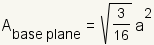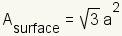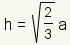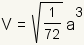Tetrahedron

Pronunciation: /ˌtɛ.trəˈhi.drən/ Explain

Click on the blue points and drag them to change the figure. Try to create a concave tetrahedron. Is it possible to make a concave tetrahedron? Why or why not? Manipulative 1 - Irregular Tetrahedron Created with GeoGebra.

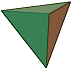
A tetrahedron is any four-sided polyhedron (see figure 1). The sides of a regular tetrahedron are equilateral triangles. Formulas for Regular Tetrahedron a is the length of an edge. Name Formula Base plane area Surface Area Height Volume Table 1

Nets for Tetrahedron

A geometric net is a 2-dimensional drawing containing polygons that can be folded into a 3-dimensional polyhedron. Figure 2 shows a net for a regular tetrahedron. Click to get a net of a regular tetrahedron you can print, cut out and fold into a tetrahedron.

Figure 2: Net of a regular tetrahedron

An irregular tetrahedron can be formed out of four triangles. Each of the triangles must have one edge the same length as each of the other three triangles. Figure 3 contains a net for an irregular tetrahedron that you can change. Click on the blue points and drag them to change the figure. To print the net, print the entire page. For best results, make your net as large as the box.

Click on the blue points and drag them to change the figure. What happens if the lines cross? Can you still build the net?

Manipulative 2 - Net of a Irregular Tetrahedron Created with GeoGebra.

Truncated Tetrahedron

Click on the blue points and drag them to change the figure. Manipulative 3 - Truncated Tetrahedron Created with GeoGebra.

A truncated tetrahedron is a tetrahedron with the vertices cut off. Figure 3 shows a regular truncated tetrahedron. Click to get a printable net of a truncated tetrahedron.

References

1. McAdams, David E.. All Math Words Dictionary, tetrahedron. 2nd Classroom edition 20150108-4799968. pg 177. Life is a Story Problem LLC. January 8, 2015. Buy the book
2. Stöcker, K.H.. The Elements of Constructive Geometry, Inductively Presented. pp 48-49. Translated by Noetling, William A.M, C.E.. www.archive.org. Silver, Burdett & Company. 1897. Last Accessed 12/16/2018. http://www.archive.org/stream/elementsofconstr00noetrich#page/48/mode/1up. Buy the book

More Information

• McAdams, David E.. Polyhedron. allmathwords.org. All Math Words Encyclopedia. Life is a Story Problem LLC. 3/12/2009. https://www.allmathwords.org/en/p/polyhedron.html.

Cite this article as:

McAdams, David E. Tetrahedron. 12/21/2018. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/t/tetrahedron.html.

Image Credits

• All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Revision History

12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
12/13/2018: Removed broken links, updated license, implemented new markup. Changed geogebra to new format. (McAdams, David E.)
8/7/2018: Changed vocabulary links to WORDLINK format. (McAdams, David E.)
12/31/2009: Added "References". (McAdams, David E.)
9/25/2008: Initial version. (McAdams, David E.)