Trigonometric Identities

Pronunciation: /ˌtrɪg.ə.nəˈmɛ.trɪk aɪˈdɛn.tə.tiz/ Explain

A trigonometric identity is a trigonometric equation that is always true. Trigonometric identities are used to solve problems involving trigonometric functions. They are particularly useful for calculus.

The common trigonometric identities are:

Pythagorean Identities

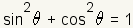cos(theta)^2+sin(theta)^2=1
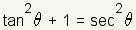tan(theta)^2+1=sec(theta)^2
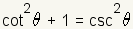cot(theta)^2+1=csc(theta)^2

Co-function Identities

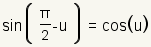sin(pi/2-u)=cos(u)
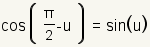cos(pi/2-u)=sin(u)
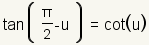tan(pi/2-u)=cot(u)
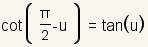cot(pi/2-u)=tan(u)
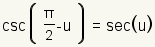csc(pi/2-u)=sec(u)
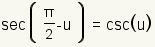sec(pi/2-u)=csc(u)

Even Odd Identities

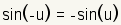sin(-u)=-sin(u)
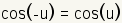cos(-u)=cos(u)
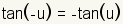tan(-u)=-tan(u)
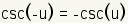csc(-u)=-csc(u)
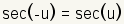sec(-u)=sec(u)
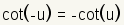cot(-u)=-cot(u)

Sum Difference Identities

sin(u+-v)=sin(u)cos(v)+-cos(u)sin(v)
cos(u+-v)=cos(u)cos(v)-+sin(u)sin(v)
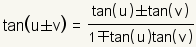tan(u+-v)=(tan(u)+-tan(v))/(1-+tan(u)tan(v)

Double Angle Identities

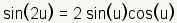sin(2u)=2sin(u)cos(u)
cos(2u)=cos^2(u)-sin^2(u)
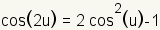cos(2u)=2cos^2(u)-1
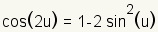cos(2u)=1-2sin^2(u)
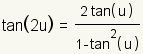tan(2u)=(2tan(u))/(1-tan^2(u))

Half Angle Identities

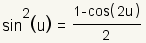sin^2(u)=(1-cos(2u))/2
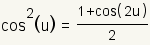cos^2(u)=(1+cos(2u))/2
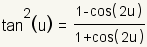tan^2(u)=(1-cos(2u)/(1+cos(2u))

Sum to Product Identities

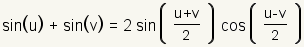sin(u)+sin(v)=2sin((u+v)/2)cos((u-v)/2)
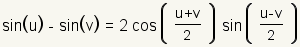sin(u)-sin(v)=2cos((u+v)/2)sin((u-v)/2)
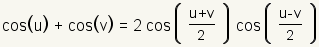cos(u)+cos(v)=2cos((u+v)/2)cos((u-v)/2)
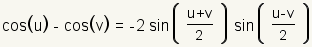cos(u)-cos(v)=-2sin((u+v)/2)sin((u-v)/2)

Product to Sum Identities

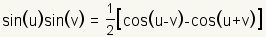sin(u)sin(v)=(1/2)(cos(u-v)-cos(u+v))
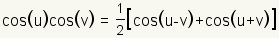cos(u)cos(v)=(1/2)(cos(u-v)+cos(u+v))
sin(u)cos(v)=(1/2)(sin(u+v)+sin(u-v))
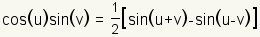cos(u)sin(v)=(1/2)(sin(u+v)-sin(u-v))
Table 1: Trigonometric identities

References

  1. McAdams, David E.. All Math Words Dictionary, trigonometric identities. 2nd Classroom edition 20150108-4799968. pg 182. Life is a Story Problem LLC. January 8, 2015. Buy the book

More Information

  • McAdams, David E.. Trigonometric Identities. allmathwords.org. All Math Words Encyclopedia. Life is a Story Problem LLC. 12/16/2018. https://www.allmathwords.org/docs/TrigonometricIdentities.pdf.

Cite this article as:

 McAdams, David E. Trigonometric Identities. 4/3/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/t/trigonometricidentities.html.

Image Credits

Revision History

4/3/2019: Removed broken links. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
12/16/2018: Removed broken links, updated license, implemented new markup. (McAdams, David E.)
1/3/2011: Added external links to derivation of Pythagorean identities and cofunction identities. (McAdams, David E.)
7/1/2008: Initial version. (McAdams, David E.)

All Math Words Encyclopedia is a service of Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License