Número complejo
Un número complejo es un número que contiene
dos porciones: una parte real y una partición “imaginaria�. La parte real es
cualquier número real. La parte imaginaria es un número real multiplicado por
la unidad imaginaria escrita como la letra minúscula
“i�. La unidad imaginaria i representa
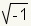 .
.
Los números complejos se escriben tÃpicamente en la forma
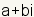 donde está a la parte real y el bi
es la partición imaginaria.
donde está a la parte real y el bi
es la partición imaginaria.
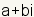 se pueden también escribir
se pueden también escribir
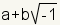 o
o
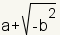
Un número imaginario es un número complejo sin parte
real, por ejemplo
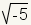 o
o
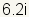 .
Esto a veces se llama un número imaginario puro.
.
Esto a veces se llama un número imaginario puro.
 Cheque de comprensión
Cheque de comprensión
Clasificar númerosPara cada número, decida qué clase o clases a las cuales cada número pertenece. Chasque “sÃâ€? o “noâ€? bajo cada clase de números. Un número puede pertenecer a más de una clase. |
|||
| Número | Complejo | Real | Imaginario puro |
|---|---|---|---|
| 6-6i | sà noEl sà está correcto. 6-6i tiene una parte real (6) y una parte imaginaria (-6i).No es incorrecto. 6-6i tiene una parte real (6) y una parte imaginaria (-6i). | sà noEl sà es incorrecto. -6i es la partición imaginaria. Un número real no tiene ninguna parte imaginaria asà que 6-6i no es un número real.No está correcto. -6i es la partición imaginaria. Un número real no tiene ninguna parte imaginaria asà que 6-6i no es un número real. | sà noEl sà es incorrecto. 6-6i tiene una parte real (6). Un número imaginario no tiene ninguna parte real asà que 6-6i no es un número imaginario.No está correcto. 6-6i tiene una parte real (6). Un número imaginario no tiene ninguna parte real asà que 6-6i no es un número imaginario. |
| 5 | sà noEl sà está correcto. 5 tiene una parte real (5). La parte imaginaria es (0i). Todos los números reals son también números complejos.El no es incorrecto. 5 tiene una parte real (5). La parte imaginaria es (0i). Todos los números reals son también números complejos. | sà noEl sà está correcto. 5 es las particiones verdaderas. Mientras que la parte imaginaria se puede considerar para ser 0i, un número complejo con 0i es también un número real.El no es incorrecto. 5 es las particiones verdaderas. Mientras que la parte imaginaria se puede considerar para ser 0i, un número complejo con 0i es también un número real. | sà noEl sà es incorrecto. 5 tiene una parte real (5). Un número imaginario no tiene ninguna parte real asà que 5 no es un número imaginario.El no está correcto. 5 tiene una parte real (5). Un número imaginario no tiene ninguna parte real asà que 5 no es un número imaginario. |
| 2i | sà noEl sà está correcto. 2i tiene una parte imaginaria (2i). La parte real es (0). Todos los números imaginarios puros son también números complejos.El no es incorrecto. 2i tiene una parte imaginaria (2i). La parte real es (0). Todos los números imaginarios son también números complejos. | sà noEl sà es incorrecto. 2i tiene una partición imaginaria. Un número real no tiene ninguna parte imaginaria, asà que 2i no puede ser imaginario.El no está correcto. 2i tiene una partición imaginaria. Un número real no tiene ninguna parte imaginaria, asà que 2i no puede ser un número real. | sà noEl sà está correcto. 2i tiene una parte imaginaria (2i). Puesto que no tiene ninguna parte real, 2i es un número imaginario.El no es incorrecto. 2i tiene una parte imaginaria (2i). Puesto que no tiene ninguna parte real, 2i es un número imaginario. |
| -3+4x | sà noEl sà es incorrecto. -3+4x es una expresión, no un número.El no está correcto. -3+4x es una expresión, no un número. | sà noEl sà es incorrecto. -3+4x es una expresión, no un número.El no está correcto. -3+4x es una expresión, no un número. | sà noEl sà es incorrecto. -3+4x es una expresión, no un número.El no está correcto. -3+4x es una expresión, no un número. |
| Cuadro 1: Clasificar números | |||
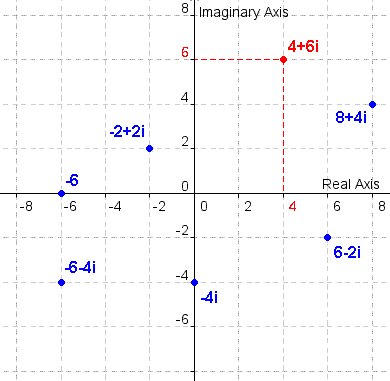
Plano complejo
|
Los números complejos se pueden representar como puntos en el plano complejo. Como el plano de cartesiano, el plano complejo tiene dos ejes: el eje real y el eje imaginario. El eje real es el eje horizontal. El eje real es también la Recta numérica real, puso en el plano complejo. El eje vertical es el eje imaginario. En el cuadro 1, encuentre el punto 4+6i, que es rojo. Observe que corresponde a 4 en el eje real y a 6 en el eje imaginario. Cada punto se traza la misma manera. Si un número no tiene ninguna parte imaginaria, es un número real, y se encuentra en el eje real. En el cuadro 1, -6 es un número real en el eje real. Si un número es un número imaginario, se encuentra en el eje imaginario. El número -4i en el cuadro 1 es un ejemplo de un número imaginario en el eje imaginario. |
Exponents de i
|
Al simplificar las expresiones que contienen el constante imaginario i, es importante saber los valores de las exponentes integrales del i. Para entender esto, recuerde la definición de i:
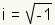 . Puesto que la función de raÃz cuadrada es lo contrario de la función cuadrada . Puesto que la función de raÃz cuadrada es lo contrario de la función cuadrada
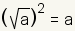 . Asà pues . Asà pues
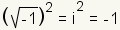 . El cuadro 1 da los valores de las primeras cinco exponentes integrales del I. ¿Puede usted imaginar los tres siguientes? Subido con su respuesta, entonces chasque encendido el “tecleo para la respuestaâ€? para comprobar su respuesta. . El cuadro 1 da los valores de las primeras cinco exponentes integrales del I. ¿Puede usted imaginar los tres siguientes? Subido con su respuesta, entonces chasque encendido el “tecleo para la respuestaâ€? para comprobar su respuesta.
|
| ||||||||||||||||||||||
Sumar de números complejos
Al sumar números complejos, agregue las piezas
correspondientes.
Sumar las partes reales juntas y las piezas imaginarias juntas:
a+bi + c+di = (a+c)+(b+d)i
Aquà están algunos ejemplos:
3+2i + 1-3i = (3+1)+(2-3)i = 4-1i = 4-i
4+1i + -2+2i = (4-2)+(1+2)i = 2+3i
Multiplicar números complejos
Para multiplicar números complejos, utilice la regla de tres:
×(a+bi)
×(c+di)
×(a·c + bi·c
×(a·c + a·di + bi·di
+ac + (ad + bc)i + bdi2
Es importante recordar que i2 = -1. Substituto -1 para i2 en la ecuación:
= ac + (ad + bc)i + bd·(-1)
= ac + (ad + bc)i - bd·
= ac - bd + (ad + bc)i
Aquà está un ejemplo:
(1-3i)·(- 6+2i)
= 1·(- 6) +1·2i+ (- 3)·(- 6) i+ (- 3)·2i2
= -6+2i+18i-6i2
= -6+20i-6i2
Substituto -1 para i2 en la ecuación:
-6+20i-6i2
= -6+20i-6(-1)
= -6+20i+6
= -6+6+20i
= 0+20i
= 20i
Propiedads de números complejos
| Propiedad | Valor | Ejemplo | Descripción |
|---|---|---|---|
| Elemento neutro de suma |
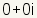
|
| La elemento neutro de la suma es el número que, cuando está sumado a cualquier
número complejo, da el número original sin cambiar. La elemento neutro de la suma para
los números complejos es
 . . |
| Identidad multiplicativa |
|
| La identidad multiplicativa es el número que, cuando es multiplicado por cualquier número complejo, da el número original sin cambiar. La identidad multiplicativa para los números complejos es
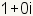 . . |
| Lo opuesto |
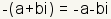
|
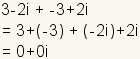
| Lo contrario del añadido de un número complejo es el número que cuando está agregado al número original da la identidad aditiva. La identidad aditiva de un número complejo arbitrario 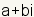 es
es 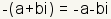 . . |
| Lo inverso multiplicativo |
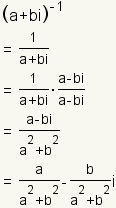
|
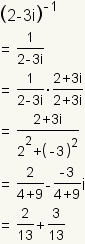
| Lo inverso multiplicativo de un número complejo es el número que cuando es multiplicado por el número original da la identidad multiplicativa. Lo inverso multiplicativo de un número complejo arbitrario
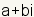 es es
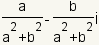 . . |
| Propiedad del asociado de la suma |
![(a+bi) + [(c+di) + (e+fi)]= [(a+bi) + (c+di)]+ (e+fi)](../../equations/c/complexnumbereqn15.png)
|
![(2-3i) + [(5 + 2i) + (- 3 - 6i)]= [(2-3i) + (5+2i)] + (- 3-6i)](../../equations/c/complexnumbereqn16.png)
| La propiedad asociativa de la suma indica que no importa la orden en la cual se agregan los números complejos. |
| Propiedad comutativa de la suma |
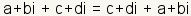
|
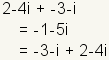
| La propiedad comutativa de la suma indica que los sumandos de números complejos pueden ser cambiados sin el cambio del resultado. |
| Propiedad del asociado de la multiplicación |
![(a+bi) * [(c+di) * (e+fi)]= [(a+bi) * (c+di)]* (e+fi)](../../equations/c/complexnumbereqn19.png)
|
![(5+2i) * [(- 3-6i) * (2-3i)]= [(5+2i) * (- 3-6i)]* (2-3i) implica (5+2i) * (- 24-3i) = (- 3-36i) * (2-3i) implica -114-63i=-114-63i.](../../equations/c/complexnumbereqn20.png)
| La propiedad asociativa de la multiplicación indica que no importa la orden en la cual se agregan los números complejos. |
| Propiedad comutativa de la multiplicación |
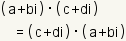
|
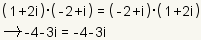
| La propiedad comutativa de la multiplicación indica que los multiplicandos de números complejos pueden ser cambiados sin el cambio del resultado. |
| Cuadro 1: Propiedads de números complejos. | |||
Adición
| El manipulante 1: Adición de números complejos. Creado con GeoGebra. |
Multiplicación
| El manipulante 2: Adición de números complejos. Creado con GeoGebra. |
Lo opuesto
| El manipulante 3: Lo opuesto de un número complejo. Creado con GeoGebra. |
Lo inverso multiplicativo
| El manipulante 4: Lo inverso multiplicativo de un número complejo. Creado con GeoGebra. |
Citar este artÃculo como:
Número complejo. 2009-04-03. Enciclopedia de Todas las Palabras de la Matemáticas. Life is a Story Problem.org. https://www.allmathwords.org/es/c/complexnumber.html.
Traducciones
créditos de imagen
- Todas las imágenes y manipulatives están por David McAdams a menos que estén indicadas de otra manera. Todas las imágenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.
La historia de revisión
2009-04-03: Traducido automáticamente por BabelFish. (babelfish.yahoo.com.)
2008-12-26: Ecuaciones cambiadas del HTML a las imágenes (McAdams, David.)
2008-07-17: Adición, multiplicación, y caracterÃsticas agregadas de números complejos (McAdams, David.)
2008-06-09: Apartado relativo agregado a números imaginarios. Imágenes cambiadas a las ecuaciones (McAdams, David.)
2008-03-25: Cambió más información al estándar actual (McAdams, David.)
2007-07-12: Versión inicial (McAdams, David.)
- Navegación
- Home
- Contenido
-
# A B C D E F G H I J L M N O P Q R S T U V X Y - Ayudas del profesor
- Demostraciones de la Clase
- Referencia recÃproca
- GeometrÃa de NYSDE
- LIASP
- LIASP Home
- Condiciones del uso
- PolÃtica de aislamiento
- Done a LIASP
- Estructura de la ayuda este sitio
- Sobre LIASP
- LIASP del Contacto
Enciclopedia de Todas las Palabras de la Matemáticas es un servicio de
Life is a Story Problem.org.
Los derechos reservados ©2005-2009 de Life is a Story Problem.org. Todos los derechos reservados.
 Este trabajo
se autoriza debajo de una
Creative Commons Attribution-Noncommercial-Share Alike 3.0 License
Este trabajo
se autoriza debajo de una
Creative Commons Attribution-Noncommercial-Share Alike 3.0 License