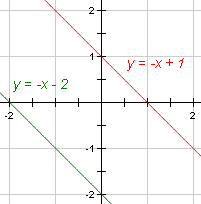Recta: Una figura unidimensional recta.

Recta

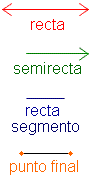
Esta imagen demuestra una recta sin puntos del extremo, un semirecta con una punto final y una recta segmento con dos puntos finales.
Cuadro 1: Una recta, semirecta
y recta segmento

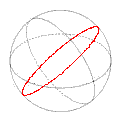
Una recta es una línea recta, unidimensional. El término unidimensional significa que la recta no tiene ninguÌ�n grueso, solamente longitud. Una recta no tiene ninguna punto final, significando que se enciende infinitamente, él se enciende por siempre. Un objeto unidimensional recto que tiene una punto final se llama un semirecta. Un objeto recto, unidimensional que tiene dos puntos finales se llama una recta segmento. Véase el cuadro 1. Una punto final es un punto en el extremo de un semirecta o de una recta segmento.

En elementos Euclid definió una recta recta como, “una recta es una línea que miente uniformemente con los puntos en sí mismo. “2 esta declaración parece confundir más que explican. Esto demuestra la dificultad en la definición de conceptos bajos. En geometría euclidiana moderna, medios “rectos� qué significamos generalmente por la palabra derecho. Se enciende sin curvar. Sin embargo, en la geometría esférica, recta significa que, aunque la recta sigue la curva de la superficie de la esfera, como en el cuadro 2, él no da vuelta a la izquierda o al right.

Esta imagen demuestra una esfera con las rectas en su superficie.
Cuadro 2: Una recta adentro
geometría esférica.

Palabras relacionadas

  • Linear: Teniendo que hacer con una recta.
  • Ecuación linear: Una ecuación linear representa una recta.
  • Sistema linear: Un sistema linear es un sistema de ecuaciones lineares relacionadas.

Contenido del artículo

Propiedad de rectas en geometría euclidiana

  • Una recta es determinada únicamente por dos points.

    La palabra significa “únicamente� que dos puntos pueden determinar solamente una recta. Cualquier recta que pase a través de los dos puntos debe ser la misma recta.

  • Dos rectas en un plano cualquiera se intersecan una vez o son paralelo.

    Dos rectas no pueden intersecarse dos veces. Si dos figuras se intersecan dos veces, por lo menos una debe curvar.

  • Dos rectas en tres o más dimensiones interseqúese, sea paralelo, o sea skew.

  • Ecuaciones de rectas

    Una ecuación que representa una recta se llama una ecuación linear. Hay varias formas acostumbradas de ecuaciones lineares:
    ax + by = cForma estándar: Se utiliza esto al representar sistemas lineares.
    y = mxVariación directa: Se utiliza esta forma cuando y cambia en la proporción con el x.
    y = mx + bForma de la pendiente-intercepción de la recta: a es la pendiente de la recta y b es y-intercepta.
    y - y1 = a(x - x1) Forma de la pendiente del punto: (x1, y1) es cualquier punto en la recta, m es la pendiente de la recta.

Pendiente de la recta

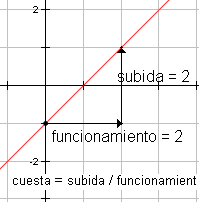
Gráfico de y = x - 1 que demuestra la pendiente es 1.
Cuadro 3: Pendiente de y = x - 1

El gráfico de y = 2x + 1 que demuestra la pendiente es 2.
Cuadro 4: Pendiente de y = 2x + 1

La pendiente de una recta es el razón de la cambie en y de la recta dividida por el cambie en x. La cambie en y refiere a la distancia vertical entre cualquier dos puntos distintos y el cambie en x refiere a la distancia horizontal entre los mismos dos puntos. La pendiente también se llama el índice de cambio. En casos de la variación directa, la pendiente también se llama el constante de la variación.

Cálculo de la pendiente de una recta

Para calcular la pendiente de una recta, primero identifique los coordenadas de cualquier dos puntos distintos. Los coordenadas del punto izquierdo más bajo en el cuadro 3 son (0, -1). Llame esto (x1, y1). Los coordenadas del punto correcto superior en el cuadro 3 son (1, 1). Llame esto (x2, y2). No importa se llama qué punto (x1, y1) y se llama cuál (x2, y2). La respuesta vendrá hacia fuera iguales.

Fórmula para pendiente es m = (y2 - y1)/(x2 - x1). Substituyendo los puntos del cuadro 3 en la fórmula, conseguimos m = (1 - (- 1)) /(2 - 0). Simplificando el numerador y el denominador, conseguimos m = 2/2 = 1. La pendiente de la recta en el cuadro 3 es tan 1.

marca de cheque Cheque de comprensión

Escriba las respuestas a los problemas siguientes en un trozo de papel. Entonces chasque encendido las palabras azules y amarillas para ver la respuesta correcta.

¿Cuál es la pendiente de la recta en el cuadro 4? Calcúlelo en el papel y después compruebe su trabajo chascando en los símbolos en amarillo en un fondo azul.

a = ( y25 - y11 ) / ( x22 - x10 ) = ( ?4 / ?2 ) = ?2.

Ã?ndice de cambio para las rectas

Al relacionarse ecuaciones lineares con el mundo real, el índice del cambio es de uso frecuente. Esto significa que dado un cambio en la variable independiente (x), uno puede aplicar el índice de cambio como razón para encontrar el cambio en la variable dependiente (y).

Marca de chequeCheque de comprensión

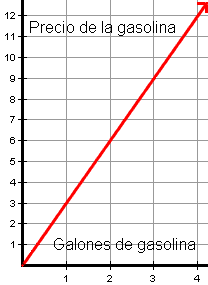
Coste total de gasolina en función del número de galones bombeados: y = 3x.
Cuadro 5: Ã?ndice de cambio

La tabla en el cuadro 5 demuestra un gráfico del coste total de gasolina en función del número de galones bombeados. Lea cada pregunta, y escriba su respuesta en un trozo de papel.

  1. ¿Si se bombea un galón, cuál es el coste total de la gasolina? Tecleo para la respuesta$3.00
  2. ¿Si se bombean dos galones, cuál es el coste total de la gasolina? Tecleo para la respuesta$6.00
  3. ¿Para cada galón se bombee que, el coste total de la gasolina va envértice de cuánto? Tecleo para la respuesta$3
  4. ¿Si se bombean los galones de x, cuál es el coste total de la gasolina? Tecleo para la respuesta$3 · x
  5. ¿Cuál es el índice de cambio para esta relación? Tecleo para la respuesta3
  6. ¿La ecuación para esta relación? Tecleo para la respuestay = 3x

Nota: El término “tarifa del cambio� tiene un similar, pero no idéntico, significando cuando está aplicado a las ecuaciones no lineares.

Los profesores, ven también el índice de lección del cambio de Cynthia Lanius.

Líneas paralelas

Gráfico del y=-x + 1 y del y=-x - 2 que demuestran que las rectas son paralelas.
Cuadro 6: Líneas paralelas

En geometría euclidiana, dos rectas son paralelas si no hacen intersecction. En geometría métrica, las rectas paralelas tienen la misma pendiente. Puesto que las dos rectas tienen el mismo índice de cambio, porque el mismo cambio en x el cambio en y será idéntico. Las rectas serán tan siempre la misma distancia aparte y nunca se intersecarán.

Rectas de intersección

Gráfico del y=-x + 1 y y=2x - 1 demostración que las rectas intersecan.
Cuadro 7: Líneas de intersección

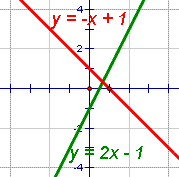
Dos rectas se intersecan si se cruzan. Otra manera de mirarlo es; dos rectas se intersecan si tienen exactamente un punto en campo común. En el cuadro 7, las dos rectas se intersecan. Puesto que el cuadro 7 es de dos dimensiones y las rectas no tienen la misma pendiente, tienen que intersecarse.

Propiedad de intersecar rectas en geometría euclidiana

  • Los ángulos opuestos son congruentes.
  • La suma de cualquier dos ángulos adyacentes es 180° = 2π.
  • Las rectas de intersección se intersecan exactamente una vez.

Encontrar los coordenadas de la intersección de rectas

Para encontrar el punto en el cual dos alinea interseqúese, substitución del uso:
EcuaciónDescripción
y=-x+1, y=2x-1Ecuaciones de las dos rectas
2x-1=-x+12x-1 substituto de la segunda ecuación para y en la primera.
3x-1=1Agregue x a ambos lados.
3x=2Agregue 1 a ambos lados.
x=2/3Divida ambos lados por 3.
y=- (2/3) + 1Substituya 2/3 adentro para x en la primera ecuación.
y=1/3Simplifique el lado derecho de la ecuación.
(x, y) = (2/3,1/3)Las rectas se intersecan en el punto (2/3,1/3)

Rectas perpendiculares

Gráfico de y=2x + 1 y y=- (el 1/2) x - 2 que demuestran que las rectas son perpendiculares.
Cuadro 8: Líneas perpendiculares
Pequeño cuadrado que denota un de ángulo llano.
Cuadro 9: Pequeño cuadrado que denota un de ángulo llano.

Dos rectas son perpendiculares si se intersecan en angles derecho. Un de ángulo llano es el 90° = π. En diagramas, los ángulos rectos se denotan con un pequeño cuadrado. Véase el cuadro 9.

En geometría métrica, usted puede decir si las rectas son perpendiculares de las pendientes. Si m1 es la pendiente de una recta, y el m2 es la pendiente de una recta perpendicular al primer, entonces m1 = -1/m2.

marca de cheque Cheque de comprensión

Un papel, completa la ecuación usada para decir si las rectas son perpendiculares usando las ecuaciones y = 2x + 1 y y = -(1/2)x - 2. ¿Son las dos rectas perpendiculares? Anote su respuesta después chasque encendido las palabras abajo para ver si su respuesta está correcta.

m12 = -1/(m2-1/2) = m12.
Las dos rectas (sea/no sea) son perpendiculares.

Sesgue las rectas

Lo sentimos, pero la GeoGebra Applet no se pudo iniciar. Por favor, asegúrese de que Java 1.4.2 (o posterior) está instalado y activo en su navegador ( Haga clic aquí para instalar Java ahora )
El manipulante 1: Líneas oblicuas. Creado con GeoGebra.

Las rectas oblicuas son las rectas que no se intersecan y no son paralelo.

En un plano euclidiano de dos dimensiones, las rectas se intersecan o son paralelas, así que las rectas de la posición oblicua no existen en espacio de dos dimensiones. Las rectas oblicuas existen solamente en espacios con tres o más dimensiones.

Manipulante 1 demuestra a los pares de rectas oblicuas en un espacio tridimensional simulado. Chasque encendido el punto azul y arrástrelo para animar el espacio.

Rectas verticales

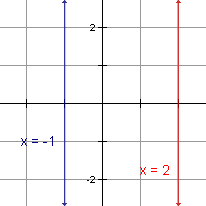
Las rectas verticales van derecho hacia arriba y hacia abajo
Cuadro 11: Líneas verticales

Una recta es vertical si va derecho hacia arriba y hacia abajo. Una recta vertical se utiliza para el eje de y al representar gráficamente. La ecuación de una recta vertical está en la forma x = b donde b está intercepta x.

Rectas horizontales

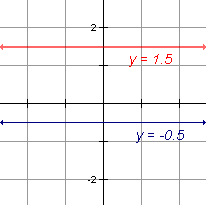
Las lineas horizontales van de lado a lado.
Cuadro 12: Lineas horizontales

Las rectas horizontales van de lado a lado. Una forma para recordar esto es recordar que el horizonte es horizontal. La ecuación de una linea horizontal se utiliza para y = b donde b está intercepta y.

Forma de la intercepción de la pendiente de ecuaciones lineares

Lo sentimos, pero la GeoGebra Applet no se pudo iniciar. Por favor, asegúrese de que Java 1.4.2 (o posterior) está instalado y activo en su navegador ( Haga clic aquí para instalar Java ahora )
El manipulante 2: Forma de la intercepción de la pendiente. Creado con GeoGebra.

La forma pendiente-intercepte de una ecuación linear es y = mx + b donde está la pendiente m de la recta y b es la y-intercepta. Una recta vertical no se puede representar en forma de la intercepción de la pendiente. Chasque encendido los puntos de los resbaladores en el manipulante 2 y arrástrelos para cambiar la figura.

Señale la forma de la pendiente de ecuaciones lineares

Lo sentimos, pero la GeoGebra Applet no se pudo iniciar. Por favor, asegúrese de que Java 1.4.2 (o posterior) está instalado y activo en su navegador ( Haga clic aquí para instalar Java ahora )
El manipulante 3: Forma de la pendiente del punto. Creado con GeoGebra.

La forma de la punto-pendiente de una ecuación linear es y - y1 = m(x - x1), donde (x1, y1) está cualquier punto en la recta y la m es la pendiente de una recta. Una recta vertical no se puede representar en forma de la pendiente del punto.

Por ejemplo, si el punto (1, 2) está en una recta con la pendiente 3, después la ecuación de la recta se puede escribir y - 2 = 3(x - 1).

Rayos

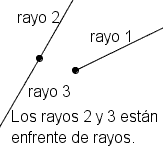
Ejemplos de semirectas.
Cuadro 15: Rayos

Un semirecta es una parte de una recta con una punto final. En la otra dirección, el semirecta se enciende por siempre, apenas como una recta. Extraiga un semirecta con un punto en un extremo que representa la punto final y una recta que irradian del otro extremo. Para demostrar que se enciende un extremo de un semirecta por siempre, dibuje una flecha. Véase el cuadro 15.

Los semirectas opuestos son los semirectas con la punto final en campo común que entran en direcciones opuestas.

Construyendo una recta segmento dado un segmento y una punto final

El manipulante 4 ayudarán a visualizar la prueba de Euclid de construir una recta segmento los mismos tamaños como recta segmento existente en un punto existente. Para cambiar el manipulante en cada paso, chasque encendido los puntos azules y arrástrelos. Para reajustar el manipulante a su condición original chasque encendido el botón Botón de reajuste de GeoGebra de reajuste en la ventana manipulante. Para demostrar los cambios para cada paso, chasque encendido el botón de la “demostración� para cada paso.

Lo sentimos, pero la GeoGebra Applet no se pudo iniciar. Por favor, asegúrese de que Java 1.4.2 (o posterior) está instalado y activo en su navegador ( Haga clic aquí para instalar Java ahora )
4 manipulantes: Copiado de una recta segmento. Creado con GeoGebra.

PasoDemostraciónDescripciónJustificación
Cargamento…
Cargamento…
Cargamento…
Cuadro 1

Más información

Para más información sobre esta construcción vea el asunto 2 del libro 1 de los elementos de Euclid: Para poner una recta recta igual a una recta recta dada con un extremo en un punto dado. Traducido por DE Joyce. http://babbage.clarku.edu/~djoyce/java/elements/bookI/propI2.html.

Referencias

1 Euclid, elementos, reserva 1 definición 2. traducida por D. Joyce. URL: http://babbage.clarku.edu/~djoyce/java/elements/bookI/defI2.html

2 Euclid, elementos, reservan 1 definición 4. traducida por D. Joyce. URL: http://babbage.clarku.edu/~djoyce/java/elements/bookI/defI4.html

3 Weisstein, geometría esférica de Eric W. De MathWorld. URL: http://mathworld.wolfram.com/SphericalGeometry.html.

4 Euclid, elementos, reservan 1 postulado 1. traducido por D. Joyce. URL: http://babbage.clarku.edu/~djoyce/java/elements/bookI/post1.html

5 Euclid, elementos, reservan 1 definición 23. Traducido por D. Joyce. URL: http://babbage.clarku.edu/~djoyce/java/elements/bookI/defI23.html

6 Weisstein, rectas oblicuas de Eric W. De MathWorld. URL: http://mathworld.wolfram.com/SkewLines.html

7 Euclid. Definición 10. del libro 1 de los elementos traducida por D. Joyce. URL: http://babbage.clarku.edu/~djoyce/java/elements/bookI/defI10.html

Más información

Euclid, elementos, reserva las definiciones 1. Traducido por D. Joyce. URL: http://babbage.clarku.edu/~djoyce/java/elements/bookI/bookI.html#defs

Weisstein, recta de Eric W. De MathWorld. URL: http://mathworld.wolfram.com/Line.html

Tabla de figuras

FiguraDescripción
Cuadro 1Una recta, un semirecta y una recta segmento
Cuadro 2Una recta en geometría esférica
Cuadro 3pendiente de y = x - 1
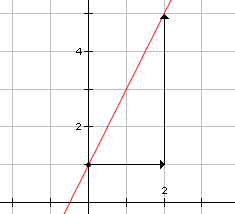
Cuadro 4pendiente de y = 2x + 1
Cuadro 5Ã?ndice de cambio
Cuadro 6Líneas paralelas
Cuadro 7Líneas de intersección
Cuadro 8Líneas perpendiculares
Cuadro 9Pequeño cuadrado que denota un de ángulo llano
Cuadro 10Líneas oblicuas
Cuadro 11Líneas verticales
Cuadro 12Lineas horizontales
Cuadro 13pendiente-intercepte la forma
Cuadro 14forma de la Punto-pendiente
Cuadro 15Rayos

Más información

  • Euclid. Elementos, Livre 1 Definición 2. babbage.clarku.edu/~djoyce. 2009-04-15. Traducido a inglés por D. Joyce. Traducido automáticamente de inglés a español por BabelFish. http://babbage.clarku.edu/~djoyce/java/elements/bookI/defI2.html.
  • Euclid. Elementos, Livre 1 Definición 4. babbage.clarku.edu/~djoyce. 2009-04-15. Traducido a inglés por D. Joyce. Traducido automáticamente de inglés a español por BabelFish. http://babbage.clarku.edu/~djoyce/java/elements/bookI/defI4.html.
  • Euclid. Elementos, Livre 1 Postulado 1. babbage.clarku.edu/~djoyce. 2009-04-15. Traducido a inglés por D. Joyce. Traducido automáticamente de inglés a español por BabelFish. http://babbage.clarku.edu/~djoyce/java/elements/bookI/post1.html.
  • Euclid. Elementos, Livre 1 Definición 23. babbage.clarku.edu/~djoyce. 2009-04-15. Traducido a inglés por D. Joyce. Traducido automáticamente de inglés a español por BabelFish. http://babbage.clarku.edu/~djoyce/java/elements/bookI/defI23.html.
  • Euclid. Elementos, Livre 1 Definición 10. babbage.clarku.edu/~djoyce. 2009-04-15. Traducido a inglés por D. Joyce. Traducido automáticamente de inglés a español por BabelFish. http://babbage.clarku.edu/~djoyce/java/elements/bookI/defI10.html.
  • Euclid. Elementos, Livre 1 Definicións. babbage.clarku.edu/~djoyce. 2009-04-15. Traducido a inglés por D. Joyce. Traducido automáticamente de inglés a español por BabelFish. http://babbage.clarku.edu/~djoyce/java/elements/bookI/bookI.html#defs.

Citar este artículo como:
Recta. 2009-04-03. Enciclopedia de Todas las Palabras de la Matemáticas. Life is a Story Problem.org. https://www.allmathwords.org/es/l/line.html.

Traducciones

créditos de imagen

  • Todas las imágenes y manipulatives están por David McAdams a menos que estén indicadas de otra manera. Todas las imágenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.

La historia de revisión


2009-04-03: Traducido automáticamente por BabelFish. (babelfish.yahoo.com.)
2008-12-05: Definición formal agregada de la punto final (McAdams, David.)
2008-11-19: Manipulatives cambiados a GeoGebra. Ayuda agregada del Javascript para la construcción una línea segmento manipulante (McAdams, David.)
2008-06-07: Faltas de mecanografíia corregidas (McAdams, David.)
2008-03-11: Ma�n acoplamiento corregido para el rayo (McAdams, David.)
2007-08-28: Agregue la referencia elementos de s de Euclid los '' (McAdams, David.)
2007-08-22: Agregue el contenido del artículo (McAdams, David.)
2007-08-21: Agregue la construcción de una línea dada una línea y una punto final (McAdams, David.)
2007-08-14: Versión inicial (McAdams, David.)

Enciclopedia de Todas las Palabras de la Matemáticas es un servicio de Life is a Story Problem.org.
Los derechos reservados ©2005-2009 de Life is a Story Problem.org. Todos los derechos reservados.
Creative Commons License Este trabajo se autoriza debajo de una Creative Commons Attribution-Noncommercial-Share Alike 3.0 License