Magnitud: La distancia de un punto a partir de la cero.

Magnitud

La magnitud de un punto en un sistema coordinado es la distancia de ese punto a partir de la cero. Para los números reales, la magnitud también se llama el valor absoluto. La magnitud (y valor absoluto) se escriben usando una recta vertical “|�.

La magnitud de x se escribe |x|. La magnitud de -7 se escribe |- 7|.

Recta numérica demostración que 3 y -3 son una distancia de tres unidades a partir de la cero.
Cuadro 1: Recta numérica demostración que 3 y -3 son una distancia de 3 a partir de la cero.

La Recta numérica en el cuadro 1 demuestra que ambos los números 3 y -3 son una distancia de 3 a partir de la cero.

Vectores

La magnitud de un vector <-3, 4> se calcula usando la fórmula de la distancia: 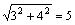raíz cuadrada (3^2+4^2)=5.

Números complejos

La definición de la magnitud se da como la distancia de un número a partir de la cero. Para los números complejos, los asimientos de la definición. Utilice la fórmula de la distancia 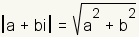|a+bi|raíz del =square (a^2+b^2), donde está la longitud a de una pierna a partir de la cero y b es la longitud de la otra pierna a partir de la cero.

Tome el número complejo 4+3i. El cuadro 2 demuestra lo que parece este punto cuando está trazado en el llano del complejo.
Número complejo 4+3i trazado en una demostración rectangular de la rejilla que la magnitud es la raíz cuadrada (4^2+3^2)=5
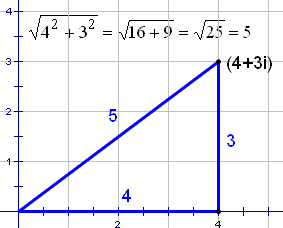Cuadro 2: El número complejo 4 + 3i trazó en el plano complejo

Podemos también utilizar la fórmula de la distancia para calcular la magnitud de 4+3i:

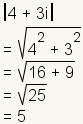
|4+3i| = raiz del quadrado (4^2+3^2) = raiz del quadrado (16+9) = raiz del quadrado (25) =5
Podemos escribir esto en una ecuación como |4 + 3i| = 5.

Observe que la magnitud es siempre positivo o póngalo a cero. Puede nunca ser negativo.

Citar este artículo como:


Magnitud. 2009-04-03. Enciclopedia de Todas las Palabras de la Matemáticas. Life is a Story Problem.org. https://www.allmathwords.org/es/m/magnitude.html.

Traducciones

créditos de imagen

  • Todas las imágenes y manipulatives están por David McAdams a menos que estén indicadas de otra manera. Todas las imágenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.

La historia de revisión


2009-04-03: Traducido automáticamente por BabelFish. (babelfish.yahoo.com.)
2008-03-11: Magnitud agregada de un vector (McAdams, David.)
2007-07-12: Versión inicial (McAdams, David.)

Enciclopedia de Todas las Palabras de la Matemáticas es un servicio de Life is a Story Problem.org.
Los derechos reservados ©2005-2009 de Life is a Story Problem.org. Todos los derechos reservados.
Creative Commons License Este trabajo se autoriza debajo de una Creative Commons Attribution-Noncommercial-Share Alike 3.0 License