Número racional
Un número racional es un número real que se puede expresar exactamente como el razón de dos números enteros.
Un número entero es siempre un número racional. Esto es porque los números enteros se pueden expresar como razón de sà mismos y 1. por ejemplo, el número 5 se puede escribir como 5/1.
En matemáticas, los números se pueden representar de las maneras que enmascaran su identidad verdadera. Por ejemplo, la raÃz cuadrada de 4 se puede reducir a 2, y asà que es un número racional, incluso si es representada usando una raÃz cuadrada.
| 5,2 | Todos los decimales finitos son números racionales. ¿Por qué? |
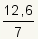 | Todas las fracciones con un numerador y un denominador racionales son números racionales. ¿Por qué? |
| 3 | Todos los números enteros son números racionales. ¿Por qué? |
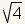 | Cualquier representación de un número que se pueda simplificar a un número racional es también un número racional. |
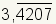 | Cualquier decimal de repetición se puede representar como fracción con numerador y denominador del número entero. Tan cualquier decimal de repetición es un número racional. |
| Cuadro 1: Representaciones de números racionales | |
 | El π se ha demostrado ser irracional. |
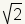 | Cualquier raÃz cuadrada que no se pueda simplificar a un número racional es irracional. |
| Cuadro 2: Representaciones de números irracionales | |
¿Por qué?
Todos los decimales finitos son números racionales.
Cualquier decimal
finito se puede representar por una fracción de números enteros. Usando la
definición de un número decimal, el número 5,2 se puede representar como
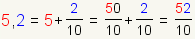
Todas las fracciones con un numerador y un denominador racionales son números racionales.
Puesto que todos los números racionales se pueden representar como
el razón de dos números enteros, la fracción
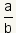se puede escribir como
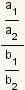donde
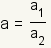y
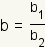. Usando las propiedads de la multiplicación,
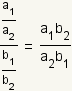desde a1, a2, b1 y
b2 son los números enteros, a1b2
y a2b1 son también números enteros,
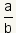son un número racional.
Todos los números enteros son números racionales.
Comience con el hecho que cualquier cosa dividido por uno sigue siendo sin cambiar. Tan
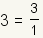puesto que 3 y 1 son números enteros,
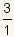es un número racional, asà que 3 deben también ser un número racional.
Cualquier raÃz cuadrada que se pueda simplificar a un número racional es un número racional.
La definición de un número racional es un número que se puede representar
como el razón de dos números enteros. Si una raÃz cuadrada se puede simplificar
a un número racional, después que la raÃz cuadrada represente un número racional.
Puesto que
,
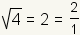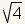representa un número racional.
Cualquier decimal de repetición es un número racional.
El decimal de repetición
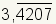se puede escribir como
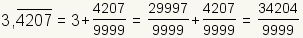. Puesto que un decimal de repetición se puede escribir como el razón de dos números enteros, todos los decimales de repetición son número racional.
Citar este artÃculo como:
Número racional. 2009-04-03. Enciclopedia de Todas las Palabras de la Matemáticas. Life is a Story Problem.org. https://www.allmathwords.org/es/r/rationalnumber.html.
Traducciones
créditos de imagen
- Todas las imágenes y manipulatives están por David McAdams a menos que estén indicadas de otra manera. Todas las imágenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.
La historia de revisión
2009-04-03: Traducido automáticamente por BabelFish. (babelfish.yahoo.com.)
2008-12-31: Ecuaciones cambiadas del hot_eqn a las imágenes (McAdams, David.)
2008-09-04: ¿Hot_Eqn agregado, agregado '' más información '', y agregado '' por qué? '' sección (McAdams, David.)
2008-03-20: Ejemplos corregidos de números irracionales (McAdams, David.)
2008-02-27: Cambie los acoplamientos calientes del vocabulario del Javascript al HTML (McAdams, David.)
2007-07-12: Versión inicial (McAdams, David.)
- Navegación
- Home
- Contenido
-
# A B C D E F G H I J L M N O P Q R S T U V X Y - Ayudas del profesor
- Demostraciones de la Clase
- Referencia recÃproca
- GeometrÃa de NYSDE
- LIASP
- LIASP Home
- Condiciones del uso
- PolÃtica de aislamiento
- Done a LIASP
- Estructura de la ayuda este sitio
- Sobre LIASP
- LIASP del Contacto
Enciclopedia de Todas las Palabras de la Matemáticas es un servicio de
Life is a Story Problem.org.
Los derechos reservados ©2005-2009 de Life is a Story Problem.org. Todos los derechos reservados.
Este trabajo
se autoriza debajo de una
Creative Commons Attribution-Noncommercial-Share Alike 3.0 License