Rational Number
Pronunciation: /ˈræʃ.nl ˈnʌm.bər/ ExplainA rational number is a real number that can be expressed exactly as the ratio of two integers.
An integer is always a rational number. This is because integers can be expressed as a ratio of themselves and 1. For example, the number 5 can be written as 5 / 1.
In math, numbers can be represented in ways that mask their true identity. For example, the square root of 4 can be reduced to 2, and so is a rational number, even if it is represented by using a square root.
| 5.2 | All finite decimals are rational numbers. Why? |
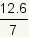 |
All fractions with a rational numerator and denominator are rational numbers. Why? |
| 3 | All integers are rational numbers. Why? |
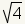 |
Any representation of a number that can be simplified to a rational number is also a rational number. |
| 3.420742074207… | Any repeating decimal can be represented as a fraction with integer numerator and denominator. So any repeating decimal is a rational number. |
| Table 1: Representations of rational numbers | |
| π | π has been proven to be irrational. |
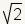 |
Any square root that can not be simplified to a rational number is irrational. |
| Table 2: Representations of irrational numbers | |
Why?
All finite decimals are rational numbers.
Any finite
decimal
can be represented by a fraction of integers. Using the definition of a decimal number,
the number 5.2 can be represented as
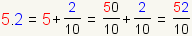
All fractions with a rational numerator and denominator are rational numbers.
Since all rational numbers can be represented as the ratio of two
integers, the fraction
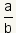 can be written as
can be written as
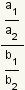 where
where
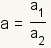 and
and
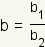 .
Using the properties of multiplication,
.
Using the properties of multiplication,
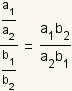 Since a1,
a2,
b1
and b2 are integers,
a1b2 and
a2b1 are also integers,
Since a1,
a2,
b1
and b2 are integers,
a1b2 and
a2b1 are also integers,
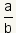 is a rational number.
is a rational number.
All integers are rational numbers.
Start with the fact that anything divided by one remains unchanged. So
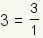 Since both 3 and 1 are
integers,
Since both 3 and 1 are
integers, 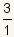 is a rational number, so 3 must also be a rational number.
is a rational number, so 3 must also be a rational number.
Any square root that can be simplified to a rational number is a rational number.
The definition of a rational number is a number that can be
represented as the ratio of two integers. If a square root can be simplified
to a rational number, then that square root represents a rational number. Since
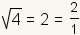 ,
,
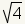 represents a rational number.
represents a rational number.
Any repeating decimal is a rational number.
The repeating decimal 3.420742074207… can be
written as
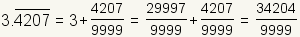 .
Since a repeating decimal can be written as the ratio of two integers,
all repeating decimals are rational number.
.
Since a repeating decimal can be written as the ratio of two integers,
all repeating decimals are rational number.
Properties of Rational Numbers
| Property | Description |
|---|---|
| Associativity | The set of rational numbers is associative with respect to addition, subtraction, multiplication and division. Example: a + (b + c) = (a + b) + c. |
| Commutativity | The set of rational numbers is commutative with respect to addition and multiplication. The set of rational numbers is not commutative with respect to subtraction or division. Example: a + b = b + a. |
| Additive identity | The additive identity for rational numbers is 0. Example: a + 0 = 0 + a = a. |
| Multiplicative identity | The multiplicative identity for rational numbers is 1. Example: a · 1 = 1 · a = a. |
| Closure | The set of rational numbers is closed with respect to addition, subtraction, multiplication, and division. Example: if a and b are rational numbers then a + b is also a rational number. |
| Discrete | The set of rational numbers is a discrete (not continuous) set. |
| Cardinality | The cardinality of the set of rational numbers is ℵ0. |
| Table 1: Properties of the rational numbers. | |
References
- McAdams, David E.. All Math Words Dictionary, rational number. 2nd Classroom edition 20150108-4799968. pg 151. Life is a Story Problem LLC. January 8, 2015. Buy the book
Cite this article as:
McAdams, David E. Rational Number. 5/2/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/r/rationalnumber.html.Image Credits
- All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Revision History
5/2/2019: Changed equations and expressions to new format. (McAdams, David E.)12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
12/5/2018: Removed broken links, updated license, implemented new markup. (McAdams, David E.)
8/7/2018: Changed vocabulary links to WORDLINK format. (McAdams, David E.)
12/19/2009: Added "References". (McAdams, David E.)
12/31/2008: Changed equations from hot_eqn to images. (McAdams, David E.)
9/4/2008: Added Hot_Eqn, added 'More Information', and added 'Why?' section. (McAdams, David E.)
3/20/2008: Corrected examples of irrational numbers. (McAdams, David E.)
2/27/2008: Change Javascript vocabulary hot links to HTML. (McAdams, David E.)
7/12/2007: Initial version. (McAdams, David E.)
- Navigation
- Home
- Contents
-
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z - Teacher Aids
- Classroom Demos
- How To
- LIASP
- LIASP Home
- Conditions of Use
- Privacy Policy
- Donate to LIASP
- Help build this site
- About LIASP
- Contact LIASP
All Math Words Encyclopedia is a service of
Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License