Angle-Angle-Side Congruence

Pronunciation: /ˈæŋ.gəl ˈæŋ.gəl saɪd kən'gru.əns/ Explain
Abbreviation: AAS

Manipulative 1 - Triangles that are congruent by AAS.

Two triangles are congruent if two adjacent angles and a side of one triangle are congruent with corresponding angles are congruent with two angles of the other triangle and a side that is not between the two angles is congruent with a corresponding side of the other triangle.[1] In this case we say that the triangles are AAS congruent. AAS stands for Angle, Angle, Side. Click on the blue points in the manipulatives and drag them to change the figures.

Proof of AAS Congruence

Step	Manipulative	Claim	Discussion
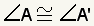
1			These are the criterion for the proof. These are assumed to be true.
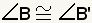
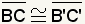
2		To show:	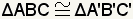This is the claim. The proof will show that the claim is true.
3		If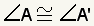 and 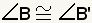then	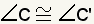If two corresponding angles of two triangles are congruent, then the third angle is congruent.
4		Since 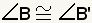and 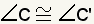and 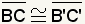, then 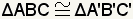. Q.E.D.	Use ASA congruence to show that the two triangles are congruent.

References

1. McAdams, David E.. All Math Words Dictionary, AAS Congruence. 2nd Classroom edition 20150108-4799968. pg 8. Life is a Story Problem LLC. January 8, 2015. Buy the book
2. Euclid. Elements. Book 1, proposition 26. Translated by Joyce, D. Clark University. Last Accessed 6/12/2018. https://mathcs.clarku.edu/~djoyce/elements/bookI/propI26.html. Buy the book

Cite this article as:

McAdams, David E. Angle-Angle-Side Congruence. 12/21/2018. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/a/aascongruence.html.

Image Credits

• All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Revision History

12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
6/12/2018: Removed broken links, updated license, implemented new markup. (McAdams, David E.)
1/4/2010: Added "References". (McAdams, David E.)
11/25/2008: Changed equations to images. (McAdams, David E.)
10/5/2008: Added proof. (McAdams, David E.)
9/16/2008: Repaired GeoGebra drawing to eliminate disappearing lines and reflex angles. (McAdams, David E.)
8/25/2007: Changed figure 1 from image to manipulative. (McAdams, David E.)
7/12/2007: Initial version. (McAdams, David E.)