Absolute Convergence
Pronunciation: /ˈæb.səˌlut kənˈvɜr.dʒəns/ ExplainA series is said to converge absolutely if the
sum of the absolute values of the
terms is convergent.[1]
In algebraic notation: A series 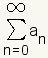 is said to converge absolutely if
is said to converge absolutely if 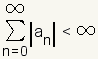 .
.
A series that converges absolutely, also converges itself. If two absolutely convergent series are multiplied together, the resulting series is also absolutely convergent.
Example
Start with the series
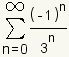 .
If the series
.
If the series
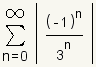 converges, then the series is absolutely convergent. Since
converges, then the series is absolutely convergent. Since
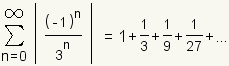 is a infinite geometric series with a ratio of
is a infinite geometric series with a ratio of
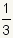 ,
it converges to
,
it converges to
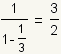 ,
So
,
So
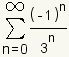 converges absolutely.
converges absolutely.
References
- McAdams, David E.. All Math Words Dictionary, absolute convergence. 2nd Classroom edition 20150108-4799968. pg 9. Life is a Story Problem LLC. January 8, 2015. Buy the book
- absolute convergence. merriam-webster.com. Encyclopedia Britannica. Merriam-Webster. Last Accessed 6/12/2018. https://www.merriam-webster.com/dictionary/absolute%20convergence. Buy the book
- Manning, Henry Parker, Ph.D.. Irrational Numbers and Their Representation by Series and Sequences. pg 89. www.archive.org. John Wiley & Sons. 1906. Last Accessed 6/12/2018. http://www.archive.org/stream/irrationalnumbe00manngoog#page/n100/mode/1up. Buy the book
More Information
- McAdams, David E.. Convergent. allmathwords.org. All Math Words Encyclopedia. Life is a Story Problem LLC. 6/19/2018. https://www.allmathwords.org/en/c/convergent.html.
- Conditional & absolute convergence. www.khanacademy.org. Kahn Academy. 6/19/2018. https://www.khanacademy.org/math/ap-calculus-bc/bc-series/bc-ratio-alt-series/v/conditional-and-absolute-convergence.
Cite this article as:
McAdams, David E. Absolute Convergence. 1/5/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/a/absoluteconvergence.html.Image Credits
- All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Revision History
1/5/2019: Corrected grammar. (McAdams, David E.)12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
6/12/2018: Removed broken links, updated license, implemented new markup. (McAdams, David E.)
1/4/2010: Added "References". (McAdams, David E.)
11/19/2008: Initial version. (McAdams, David E.)
- Navigation
- Home
- Contents
-
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z - Teacher Aids
- Classroom Demos
- How To
- LIASP
- LIASP Home
- Conditions of Use
- Privacy Policy
- Donate to LIASP
- Help build this site
- About LIASP
- Contact LIASP
All Math Words Encyclopedia is a service of
Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License