Geometric Series
Pronunciation: /ˌdʒi.əˈmɛt.rɪk ˈsɪər.iz/ ExplainA geometric series is a series with a common ratio between successive terms. The common ratio is a constant. For example, the series 1 + 2 + 4 + 8 + … is a geometric series. The constant ratio between each term is 2: (1 · 2 = 2; 2 · 2 = 4; 4·2 = 8; …...).
A geometric series S can written in the notation where
a is the first term, and r is the constant ratio. If the first term
is 2 and the constant ratio is
where
a is the first term, and r is the constant ratio. If the first term
is 2 and the constant ratio is
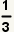 ,
the geometric series is
,
the geometric series is

Sum
The sum of a geometric series is the sum of each of the terms of the geometric series. A partial sum is a sum of the first n terms of the geometric series. The notation for a partial sum of the first n terms of a geometric series is written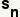 .
The partial sum of the first four terms of the series
.
The partial sum of the first four terms of the series
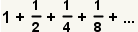 is:
is:
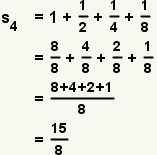
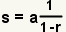 .
.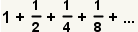 is:
is:
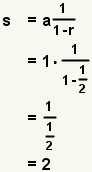 .
.Properties
- If 0 < r < 1, successive terms become smaller and smaller, getting closer to zero. The sum can be found using the formula
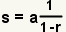
- If r = 1, all terms are the same value. The sum does not exist.
- If r > 1, successive terms become bigger and bigger, approaching infinity. The sum does not exist.
- if r = -1, successive terms are additive inverses (a, -a, a, -a, ...), the partial sums of the terms oscilates. The sum does not exist.
Graphical Representation of Geometric Series
|
Click on the points on the sliders in the upper left corner and drag them to change the figure. |
| Manipulative 1 - Geometric Series Created with GeoGebra. |
References
- McAdams, David E.. All Math Words Dictionary, geometric series. 2nd Classroom edition 20150108-4799968. pg 85. Life is a Story Problem LLC. January 8, 2015. Buy the book
- geometric series. Merriam-Webster Online Dictionary. Merriam-Webster. Last Accessed 12/26/2018. https://www.merriam-webster.com/dictionary/geometric%20series. Buy the book
- Bettinger, Alvin K. and Englund, John A.. Algebra And Trigonometry. pp 265-267. www.archive.org. International Textbook Company. January 1963. Last Accessed 7/11/2018. http://www.archive.org/stream/algebraandtrigon033520mbp#page/n282/mode/1up/search/progression. Buy the book
- Young, J. W. A. and Jackson, Lambert L.. A Second Course in Elementary Algebra. pp 174-177. www.archive.org. D. Appleton and Company. 1910. Last Accessed 7/11/2018. http://www.archive.org/stream/secondcourseinel00younrich#page/174/mode/1up/search/progression. Buy the book
More Information
- Knaust, Helmut. The Geometric Series. sosmath.com. SOS Math. 12/1/2009. http://www.sosmath.com/calculus/geoser/geoser01.html.
Cite this article as:
McAdams, David E. Geometric Series. 4/21/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/g/geometricseries.html.Image Credits
- All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Revision History
4/21/2019: Updated equations and expressions to new format. (McAdams, David E.)12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
8/7/2018: Changed vocabulary links to WORDLINK format. (McAdams, David E.)
7/10/2018: Removed broken links, updated license, implemented new markup, implemented new Geogebra protocol. (McAdams, David E.)
2/6/2010: Added "References". (McAdams, David E.)
12/1/2009: Initial version. (McAdams, David E.)
- Navigation
- Home
- Contents
-
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z - Teacher Aids
- Classroom Demos
- How To
- LIASP
- LIASP Home
- Conditions of Use
- Privacy Policy
- Donate to LIASP
- Help build this site
- About LIASP
- Contact LIASP
All Math Words Encyclopedia is a service of
Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License