Circle
Pronunciation: /ˈsɜr.kəl/ Explain
|
A circle is all points in a plane that are equidistant from the center point. When using a compass to draw a circle, the point of the compass is the center of the circle, and the stylus marks all points that are the same distance from the center. |
Properties of a Circle
Click on the blue points in manipulative 1 and drag them to change the figure. Double click on the manipulative to open it in a full-screen window.
|
|
 Understanding Check
Understanding Check
- Is a diameter also a chord? Try moving the endpoints of the chord in figure 2 on top
of the endpoints of the diameter.
 Yes.
Yes.
Correct. Since a chord is a line between any two points on the circle, and a diameter is a line between a point and a point opposite that point, a diameter is a special case of a chord. No.
No.
Incorrect. Since a chord is a line between any two points on the circle, and a diameter is a line between a point and a point opposite that point, a diameter is a special case of a chord. - Does each circle have exactly one diameter? Try moving the endpoints of the diameter in figure 2.
 Yes.
Yes.
Incorrect. Each circle has an infinite number of points on its circumference, it also has an infinite number of diameters. However, all of the diameters of a circle have the same measure. No.
No.
Correct. Each circle has an infinite number of points on its circumference, it also has an infinite number of diameters. However, all of the diameters of a circle have the same measure. - What is the relationship between the measure of a radius and the measure of a diameter of a circle?
 The measure of a radius has no relationship to the measure of a diameter.
The measure of a radius has no relationship to the measure of a diameter.
Incorrect. A radius goes halfway across a circle. A diameter goes all the way across a circle. So the measure of a radius is 1/2 the measure of a diameter. The measure of a radius is 1/4 the measure of a diameter.
The measure of a radius is 1/4 the measure of a diameter.
Incorrect. A radius goes halfway across a circle. A diameter goes all the way across a circle. So the measure of a radius is 1/2 the measure of a diameter. The measure of a radius is 1/2 the measure of a diameter.
The measure of a radius is 1/2 the measure of a diameter.
Correct. A radius goes halfway across a circle. A diameter goes all the way across a circle. So the measure of a radius is 1/2 the measure of a diameter. The measure of a radius is exactly the same as the measure of a diameter.
The measure of a radius is exactly the same as the measure of a diameter.
Incorrect. A radius goes halfway across a circle. A diameter goes all the way across a circle. So the measure of a radius is 1/2 the measure of a diameter.
Formulas Related to a Circle
| Definitions of Variables | |
|---|---|
| Variable | Represents |
| r | radius |
| d | diameter |
| c | circumference |
| a | area |
| h | x-coordinate of the center of a circle |
| k | y-coordinate of the center of a circle |
| Description | Equation |
| Diameter of a circle | d = 2r |
| Circumference of a circle | c = 2πr |
| Area of a circle | a = πr2 |
| Equation for a circle in Cartesian coordinates | (x - h)2 + (y - k)2 = r2 |
| Equation of a circle with center at the origin in Polar coordinates | r = r0 |
| Table 1: Formulas relating to a circle | |
Center-Radius Equation of a Circle
|
The center-radius equation of a circle is (x - h)2 + (y - k)2 = r2. In this equation the point (h, k) is the coordinates of the center of the circle, and r is the radius of the circle. |
How to Plot a Circle
For this demonstration use the center-radius equation for a circle centered at (-1, 2): (x + 1)2 + (y - 2)2 = (1.5)2.
| Step | Diagram | Description |
|---|---|---|
| 1 | 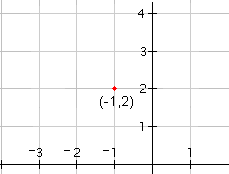 |
Since x - h = x + 1, h = -1. Since y - k = y - 2, k = 2. So the center of the circle is at the point (-1, 2). Plot the point (-1, 2). |
| 2 | 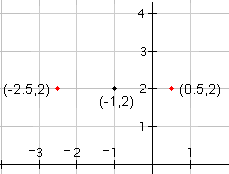 |
Now draw the two points that are on the circle to the right and left of the center. Since the radius is 1.5, the left point will be at (-1 - 1.5, 2) = (-2.5, 2) (the x-coordinate of the center of the circle minus the radius). The right point will be at (-1 + 1.5, 2) = (0.5, 2) (the y-coordinate of the center of the circle plus the radius). |
| 3 | 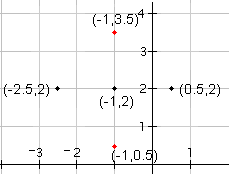 |
Now draw the two points that are on the circle that are on the top and bottom of the center. Since the radius is 1.5, the top point will be at (-1, 2 + 1.5) = (-1, 3.5) (the y-coordinate of the center of the circle plus the radius). The bottom point will be at (-1, 2 - 1.5) = (-1, 0.5) (the y-coordinate of the center of the circle minus the radius). |
| 4 | 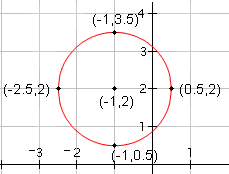 |
Now, draw a circle through the four points. |
References
- McAdams, David E.. All Math Words Dictionary, circle. 2nd Classroom edition 20150108-4799968. pg 33. Life is a Story Problem LLC. January 8, 2015. Buy the book
More Information
- McAdams, David E.. Conic Section. allmathwords.org. Life is a Story Problem LLC. 6/27/2018. https://www.allmathwords.org/en/c/conicsection.html.
Educator Resources
- Circumference and More Geometry. NASA LaRC Office of Education. 2/18/2010. http://www.archive.org/details/NasaConnect-Eom-CircumferenceAndMoreGeometry/index.htm.
Cite this article as:
McAdams, David E. Circle. 4/13/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/c/circle.html.Image Credits
- All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
- Using a compass to draw a circleGeoTeach.com. Used by permission.
Revision History
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)6/25/2018: Removed broken links, updated license, implemented new markup, updated GeoGebra apps. (McAdams, David E.)
1/27/2010: Expanded parts of a circle to include sector, segment, tangent, point of tangency, and tangent segment. Expanded verbiage on center-radius equation of a circle. (McAdams, David E.)
12/28/2009: Added "References". (McAdams, David E.)
11/25/2008: Added link to chord.html in 'Parts of a Circle' (McAdams, David E.)
10/27/2008: Changed manipulative from geometer's sketchpad to geogebra. Corrected formula for the area of a circle. Added manipulative for the equation of a circle (McAdams, David E.)
4/28/2008: Added section on plotting a circle. Added conic section to more info (McAdams, David E.)
7/12/2007: Initial version. (McAdams, David E.)
- Navigation
- Home
- Contents
-
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z - Teacher Aids
- Classroom Demos
- How To
- LIASP
- LIASP Home
- Conditions of Use
- Privacy Policy
- Donate to LIASP
- Help build this site
- About LIASP
- Contact LIASP
All Math Words Encyclopedia is a service of
Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License
