Conic Section

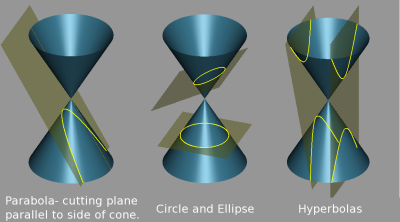
Pronunciation: /ˈkɒn.ɪk ˈsɛk.ʃən/ Explain

A conic section is a 2-dimensional figure formed by intersecting the surface of a 3-dimensional double cone with a plane (see figure 1).^[2] Four 2-dimensional figures that can be formed are the circle, ellipse, parabola, and hyperbola. Conic sections were studied as early as 200 BC by Apollonius of Perga.

Figure 1: Conic Sections. Courtesy Duk@en.Wikipedia.org. Licensed under the GNU Free Documentation License.

Figure 2: Table of Conics, Cyclopaedia, 1728. Click on picture to see full size.

References

1. McAdams, David E.. All Math Words Dictionary, conic section. 2nd Classroom edition 20150108-4799968. pg 43. Life is a Story Problem LLC. January 8, 2015. Buy the book
2. conic section. merriam-webster.com. Encyclopedia Britannica. Merriam-Webster. Last Accessed 6/25/2018. http://www.merriam-webster.com/dictionary/conic section. Buy the book
3. Drew, Rev. W. H.. A geometrical treatise on conic sections. 4th edition. www.archive.org. MacMillan and Company. 1869. Last Accessed 6/25/2018. http://www.archive.org/stream/cu31924031271509#page/n6/mode/1up. Buy the book
4. Hamilton, Rev. Henry Parr. An Analytical System of Conic Sections. 5th edition. article 79-80. www.archive.org. John W. Parker. 1863. Last Accessed 6/25/2018. http://www.archive.org/stream/ananalyticalsys00hamigoog#page/n93/mode/1up/search/conic. Buy the book

Cite this article as:

McAdams, David E. Conic Section. 12/21/2018. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/c/conicsection.html.

Image Credits

• All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
• Conic Sections: Pietros Sacanis, https://commons.wikimedia.org. Released into public domain by author. https://commons.wikimedia.org/wiki/File:Conic_sections_sk.png.
• Table of Conicks: Unknown, https://commons.wikimedia.org. This work is in the public domain in its country of origin and other countries and areas where the copyright term is the author's life plus 70 years or less. https://commons.wikimedia.org/wiki/File:Table_of_Conics,_Cyclopaedia,_volume_1,_p_304,_1728.jpg#file.

Revision History

12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
6/25/2018: Removed broken links, updated license, implemented new markup, updated GeoGebra apps. (McAdams, David E.)
10/11/2008: Changed definition to refer to the 'surface' of a double cone. (McAdams, David E.)
7/7/2008: Corrected link errors. Corrected spelling (McAdams, David E.)
4/28/2008: Initial version. (McAdams, David E.)