Cramer's Rule

Pronunciation: /ˈkreɪmərz rul/ Explain

Cramer's rule is an algorithm for solving square linear systems using determinants of matrices.[2] Cramer's rule can only be used with linear systems that have exactly one solution. Cramer's rule is named after Gabriel Cramer (1704–52), a Swiss mathematician.

Cramer's rule uses determinants to find the solution of a linear system. For example, start with the linear system

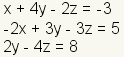
x+4y-2z=3, -2x+3y-3z=5, 2y-4z=8
Now convert this linear system into a 3x4 matrix.
3x4 matrix first row 1,4,-2,3; second row -2,3,-3,5; third row 0,2,-4,8
We will be making four determinants out of this matrix. Each of these determinants will be based on a 3x3 square matrix. The first determinant, which we will label |A0|, is the first three columns of the matrix.
determinant of 3x3 matrix named A0 first row 1,4,-2; second row -2,3,-3; third row 0,2,-4
Now find the value of |A0|.
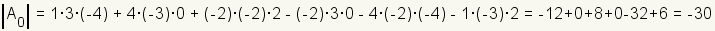
determinant of A0 is 1*3*(-4)+4*(-3)*0+(-2)*(-2)*2-(-2)*3*0-4*(-2)*(-4)-1*(-3)*2=-12+0+8+0-32+6=-30
The second determinant will be based on the first. Substitute the last column of matrix A into the first column of determinant |A0|. The new determinant is labeled |Ax|.
determinant of 3x3 matrix named Ax first row -3,4,-2; second row 5,3,-3; third row 8,2,-4
Now find the value of |Ax|.
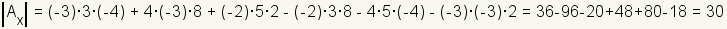
determinant of Ax is (-3)*3*(-4)+4*(-3)*8+(-2)*5*2-(-2)*3*8-4*5*(-4)-(-3)*(-3)*2=36-96-20+48+80-18=30
Continue by finding the determinate of |Ay|. Do this by substituting the last column of matrix A into the second column of determinant |A0|.
determinant of 3x3 matrix named Ay first row 1,-3,-2; second row -2,5,-3; third row 0,8,-4
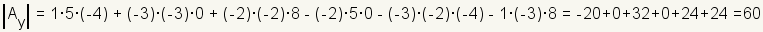
determinant of Ay is 1*5*(-4)+(-3)*(-3)*0+(-2)*(-2)*8-(-2)*5*0-(-3)*(-2)*(-4)-1*(-3)*8=-20+0+32+0+24+24=60
Now repeat the pattern for |Az|.
determinant of 3x3 matrix named Az first row 1,4,-3; second row -2,3,5; third row 0,2,8
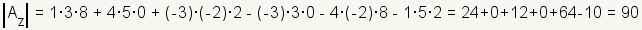
determinant of Az is 1*3*8+4*5*0+(-3)*(-2)*2-(-3)*3*0-4*(-2)*8-1*5*2=24+0+12+0+64-10=90
The solution for the linear system is
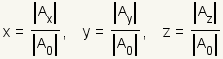
x=|Ax|/|A0|, y=|Ay|/|A0|, z=|Az|/|A0|
So
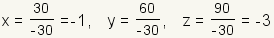
x=30/(-30)=-1, y=60/-30=-2, z=90/-30=-3

References

  1. McAdams, David E.. All Math Words Dictionary, Cramer's rule. 2nd Classroom edition 20150108-4799968. pg 50. Life is a Story Problem LLC. January 8, 2015. Buy the book
  2. Skinner, Ernest Brown. College Algebra. pp 92-93. www.archive.org. The Macmillan Company. 1917. Last Accessed 6/25/2018. http://www.archive.org/stream/cu31924031226503#page/n103/mode/1up/search/cramer. Buy the book
  3. Householder, Alston S.. Principles Of Numerical Analysis. pp 28-29. www.archive.org. McGraw-Hill Book Company, Inc.. 1953. Last Accessed 6/25/2018. http://www.archive.org/stream/principlesofnume030218mbp#page/n47/mode/1up/search/cramer. Buy the book

More Information

  • McAdams, David E.. Determinant. allmathwords.org. All Math Words Encyclopedia. Life is a Story Problem LLC. 6/27/2018. https://www.allmathwords.org/en/d/determinant.html.

Cite this article as:

 McAdams, David E. Cramer's Rule. 12/21/2018. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/c/cramersrule.html.

Image Credits

Revision History

12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
6/25/2018: Removed broken links, updated license, implemented new markup, updated GeoGebra apps. (McAdams, David E.)
1/22/2010: Added "References". (McAdams, David E.)
12/27/2008: Corrected url in citation. (McAdams, David E.)
7/1/2008: Initial version. (McAdams, David E.)

All Math Words Encyclopedia is a service of Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License