Determinant of a Matrix

Pronunciation: /dɪˈtɜr.mə.nənt ʌv ə ˈmeɪ.trɪks/ Explain

A determinant of a square matrix is a value calculated from the elements of the matrix.^[3] A determinant is defined only for a square matrix. The determinant of matrix A is denoted |A| or det(A).

How to Calculate the Determinant of a Matrix

A determinant is calculated by multiplying the diagonals of the matrix, then adding or subtracting the products of the diagonals. For the 2x2 matrix

multiply the diagonal from the upper left to lower right first (b₁₁ · b₂₂). Then multiply the diagonal from the upper right to the lower left (b₁₂ · b₂₁). Subtract the second product from the first (b₁₁ · b₂₂ - b₁₂ · b₂₁). This is the determinant of the matrix.

Example 1

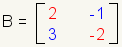
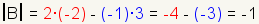
Determinant of a 3x3 matrix

Figure 1 shows how to find the determinant of a 3x3 matrix.. The first diagonals go from top left to bottom right. The numbers multiplied are a₁₁ · a₂₂ · a₃₃, then a₁₂·a₂₃·a₃₁, then a₁₃·a₂₁·a₃₂. The product of these diagonals are added together.

The diagonals from upper right to bottom left are calculated. The numbers multiplied are a₁₃·a₂₂·a₃₁, then a₁₂·a₂₁·a₃₃, then a₁₁·a₂₃·a₃₂. These products are subtracted from the previous sum.

The function for the determinant of a 3x3 matrix is |A| = a₁₁·a₂₂·a₃₃ + a₁₂·a₂₃·a₃₁ + a₁₃·a₂₁·a₃₂ - a₁₃·a₂₂·a₃₁ - a₁₂·a₂₁·a₃₃ - a₁₁·a₂₃·a₃₂.

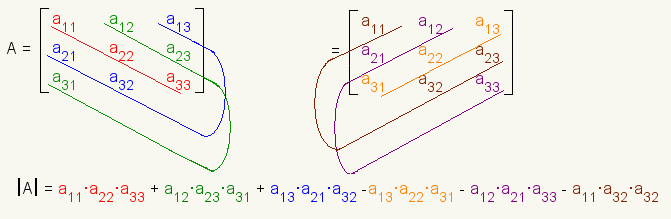
Figure 1: The determinant of a 3x3 matrix

Example 2

References

1. McAdams, David E.. All Math Words Dictionary, determinant. 2nd Classroom edition 20150108-4799968. pg 58. Life is a Story Problem LLC. January 8, 2015. Buy the book
2. determinant. merriam-webster.com. Encyclopedia Britannica. Merriam-Webster. Last Accessed 7/3/2018. http://www.merriam-webster.com/dictionary/determinant. Buy the book
3. Ferrar, W. L.. Algebra: A Text-Book of Determinants, Matrices, and Algebraic Forms. 2nd edition. www.archive.org. NULl. Oxford University Press. 1960. Last Accessed 7/3/2018. http://www.archive.org/stream/algebra032104mbp#page/n10/mode/1up/search/determinant. Buy the book
4. Bôcher, Maxime. Introduction to Higher Algebra. pp 20-26. www.archive.org. The Macmillan Company. July 1947. Last Accessed 7/3/2018. http://www.archive.org/stream/cu31924002936536#page/n35/mode/1up/search/determinant. Buy the book
5. Ferrar, W. L.. Algebra. 2nd edition. pp 5-66. www.archive.org. Oxford University Press. 1960. Last Accessed 7/3/2018. http://www.archive.org/stream/algebra032104mbp#page/n14/mode/1up/. Buy the book

More Information

• McAdams, David E.. Matrix. allmathwords.org. All Math Words Encyclopedia. Life is a Story Problem LLC. 3/12/2009. https://www.allmathwords.org/en/m/matrix.html.

Cite this article as:

McAdams, David E. Determinant of a Matrix. 4/20/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/d/determinant.html.

Image Credits

• All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Revision History

4/20/2019: Updated equations and expressions to the new format (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
7/4/2018: Removed broken links, updated license, implemented new markup, implemented new Geogebra protocol. (McAdams, David E.)
1/23/2010: Added "References". (McAdams, David E.)
1/9/2009: Added Laplace Expansion to 'More Information'. (McAdams, David E.)
12/27/2008: Changed '3xe matrix' to '3x3 matrix'. (McAdams, David E.)
12/3/2008: Initial version. (McAdams, David E.)