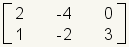Matrix

Pronunciation: /ˈmeɪ.trɪks/ Explain

-- plural is matrices.

Figure 1: 2x3 matrix

A matrix is made up of values arranged in rows and columns. In advanced math, the values can be variables, equations or even other matrices. This article will deal with matrices that contain only numbers.

Article Index

Matrix
Matrix Rows and Columns
Matrix Dimension
Square Matrix
Diagonal of a Square Matrix
Augmented Matrix
Matrix Element
Corresponding Elements
Equality of Matrices
Matrix Addition
Scalar Multiplication
Matrix Multiplication
Determinant of a Matrix
Cramer's Rule

Matrix

A matrix is used to organize data. Once data is organized into a matrix, standard matrix operations can be performed to manipulate the data. Here is an example from retail sales. Table 1 contains sales information for the first three months of the year for a store. Table 2 contains sales information for the second three months of the year for the same store.

1st Quarter Sales, Store #482 January February March Fruit $3045 $2997 $3200 Vegetables $4056 $4227 $4509 Pasta $2650 $3204 $3098 Dairy $5345 $4723 $4933 Figure 2: Table of first quarter sales.

2nd Quarter Sales, Store #482 April May June Fruit $3420 $3560 $3700 Vegetables $4716 $4850 $4900 Pasta $3274 $2840 $2760 Dairy $4769 $4799 $4873 Figure 3: Table of second quarter sales.

These tables 1 and 2 can be organized into two matrices:

Figure 4: Matrix corresponding to table in figure 2.

Figure 5: Matrix corresponding to table in figure 3.

Notice that none of the labels are transferred to the matrix. However, the numbers in the rows and columns still have the same meaning. Everything in the first row is sales numbers for fruit. Everything in the second row is sales numbers for vegetables. Everything in the first column is the sales for the first month of the quarter.

Understanding Check

Click on the check box of the answer you think is correct.

1. What is the meaning of matrix 2, row 3?
   Sales of fruit.
   No, since row 3 of matrix 2 corresponds to row three of table 2, row 3 represents sales of pasta.
   Sales of vegetables.
   No, since row 3 of matrix 2 corresponds to row three of table 2, row 3 represents sales of pasta.
   Sales of pasta.
   Yes, since row 3 of matrix 2 corresponds to row three of table 2, row 3 represents sales of pasta.
   Sales of dairy products.
   No, since row 3 of matrix 2 corresponds to row three of table 2, row 3 represents sales of pasta.
2. What is the meaning of matrix 1, column 2?
   January sales.
   No, since column 2 of matrix 1 corresponds to column 2 of table 2, row 3 represents February sales.
   February sales.
   Yes, since column 2 of matrix 1 corresponds to column 2 of table 2, row 3 represents February sales.
   May sales.
   No, since column 2 of matrix 1 corresponds to column 2 of table 2, row 3 represents February sales.
   June sales.
   No, since column 2 of matrix 1 corresponds to column 2 of table 2, row 3 represents February sales.
3. What is the meaning of matrix 1, column 1, row 2?
   Sales of fruit in January.
   No, since column 1, row 2 of matrix 1 corresponds to column 1, row 2 of table 1, this cell represents sales of vegetables in January.
   Sales of vegetables in March.
   No, since column 1, row 2 of matrix 1 corresponds to column 1, row 2 of table 1, this cell represents sales of vegetables in January.
   Sales of fruit in April.
   No, since column 1, row 2 of matrix 1 corresponds to column 1, row 2 of table 1, this cell represents sales of vegetables in January.
   Sales of vegetables in January.
   Yes, since column 1, row 2 of matrix 1 corresponds to column 1, row 2 of table 1, this cell represents sales of vegetables in January.

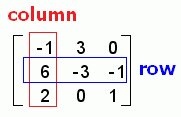
A Matrix is Organized in Columns and Rows

Matrix rows and columns.

A matrix is organized in columns and rows. A column is a single vertical arrangement of values. A row is a single horizontal arrangement of values. A matrix can have one or more columns and one or more rows. If the values in the matrix represent real data, each column and each row has meaning.

Matrix Dimension

Each matrix has a dimension. Since the matrix 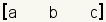has 1 row and 3 columns, the dimensions of this matrix are 1x3.

Matrix	Number of Rows	Number of Columns	Dimensions
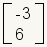	2	1	2x1
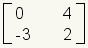	2	2	2x2
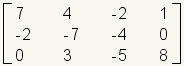	3	4	3x4
Figure 6: Dimensions of Matrices

Square Matrix

Figure 7: A square 2x2 matrix

A square matrix is a matrix that has the same number of rows as columns. One property of a square matrix is that a square matrix can be multiplied by itself. This is not true for matrices that are not square.

Diagonal of a Square Matrix

Figure 8: The diagonal of a 3x3 matrix

The diagonal of a square matrix A is the elements A1,1, A2,2, A3,3, …. In figure 8, the diagonal is highlighted in red. Some mathematicians call the diagonal of a matrix a main diagonal.

Augmented Matrix

Figure 8a: An augmented matrix.

An augmented matrix is a square matrix with a column added. An augmented matrix is used to represent a linear system. Each column of the square matrix represents a variable. The augmented part of the matrix represents the constant term of each linear equation. An augmented matrix is sometimes represented using a vertical line to separate the square matrix from the augmented part. See figure 8b.

Figure 8b: Augmented matrix with a vertical separator.

Matrix Element

Figure 9: Matrix A

Each entry in a matrix is called a matrix element. Each element is identified by row and column in the array. The highlighted element in matrix A is identified as A[2,1]. This means the element in the second row, first column of matrix A.

Understanding Check

Click on the check box of the answer you think is correct.

1. What is the value of the element A[3,2]?
   1
   No. The element in row 3 (count down 3 rows) and column 2 (count over 2 columns) has a value of 4.
   4
   Yes. The element in row 3 (count down 3 rows) and column 2 (count over 2 columns) has a value of 4.
   5
   No. The element in row 3 (count down 3 rows) and column 2 (count over 2 columns) has a value of 4.
   8
   No. The element in row 3 (count down 3 rows) and column 2 (count over 2 columns) has a value of 4.
2. What is the value of the element A[1,3]?
   1
   No. The element in row 1 (count down 1 row) and column 3 (count over 3 columns) has a value of 7.
   3
   No. The element in row 1 (count down 1 row) and column 3 (count over 3 columns) has a value of 7.
   5
   No. The element in row 1 (count down 1 row) and column 3 (count over 3 columns) has a value of 7.
   7
   Yes. The element in row 1 (count down 1 row) and column 3 (count over 3 columns) has a value of 7.
3. What element of Matrix A has a value of 1?
   A[1,1]
   No. The element A[2,2] = 1.
   A[1,2]
   No. The element A[2,2] = 1.
   A[2,1]
   No. The element A[2,2] = 1.
   A[2,2]
   Yes. The element A[2,2] = 1.

Corresponding Elements

Corresponding elements in matrices are elements at the same row and column. In figure 10, corresponding elements of the two matrices are the same color.

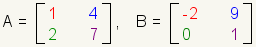Figure 10: Corresponding elements

Equality of Matrices

Two matrices are equal if and only if two conditions are met:

1. The matrices have exactly the same number of rows and columns.
2. The corresponding elements of the matrices are equal.

Examples of Matrix Equality

Example	Discussion
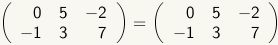	These two matrices are equal. They have the same number of rows and the same number of columns and their corresponding elements are equal.
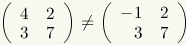	These matrices are not equal. The have the same number of rows and the same number of columns, but the elements in position 1,1 are not equal.
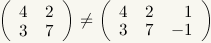	These matrices are not equal. While the corresponding elements are equal, the first matrix has two columns and the second matrix has three columns.
Table 11 - Examples of matrix equality.

Matrix Addition

Matrix addition is defined as adding corresponding elements. Let matrix

and matrix To add the matrix B to C, add the value of B[1,1] to C[1,1], B[1,2] to C[1,2], and so on as follows:

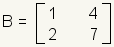
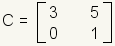
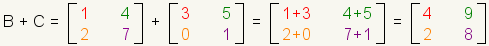Figure 12: Matrix addition

Since each element in the first matrix must have a corresponding element in the second matrix, only matrices with the same dimensions can be added. Addition of matrices with different dimensions is undefined. This means that you can not add matrices with different dimensions.

Matrix subtraction is similar to matrix addition. Subtract corresponding elements.

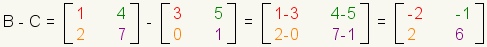Figure 13: Matrix subtraction

Scalar Multiplication

Figure 14: Scalar multiplication

In scalar multiplication, a scalar is a number that is multiplied by each element of the matrix. Figure 13 shows the scalar 5 being multiplied by a matrix. Each element of the matrix is multiplied by five.

Matrix Multiplication

Matrix multiplication is defined as multiplying the elements of each row of the first matrix by each column of the second matrix. Figure 15 shows an example of matrix multiplication.

Figure 15: Matrix multiplication.

To multiply two matrices, they must be compatible. This means that the number of columns in the first matrix must be the same as the number of rows in the second matrix. Figure 16 gives some examples of compatible and incompatible matrices.

Matrix 1	Matrix 2	Compatibility
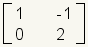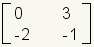		Compatible. These matrices are compatible. They can be multiplied. The first matrix has 2 columns and the second matrix has 2 rows.
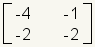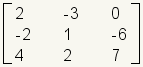		Incompatible. These matrices are incompatible. They can not be multiplied. The first matrix has 2 columns and the second matrix has 3 rows.
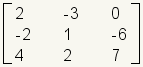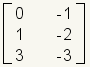		Compatible. These matrices are compatible. They can be multiplied. The first matrix has 3 columns and the second matrix has 3 rows.
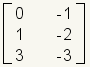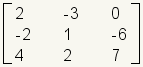		Incompatible. These matrices are incompatible. They can not be multiplied. The first matrix has 2 columns and the second matrix has 3 rows. Note: These are the same matrices in the previous example, but have been reversed. This means that matrix multiplication is not commutative.
Figure 16: Matrix compatibility

It is easier to remember how to multiply matrices if you move the second matrix up. Take, for example, the matrix multiplication problem:

The second matrix is moved up like this: Now the columns and rows of the matrices that will be multiplied are aligned. Start with row 1 and column 1 of the matrix. The elements in the first row of the first matrix are multiplied by the elements in the first column of the second matrix: 2 · 0 + (-3) · 1 + 0 · 3 = 0 - 3 + 0 = -3. Now multiply row 1 of matrix 1 by column 2 of matrix 2. 2 · (-1) + (-3) · 2 + 0 · (-3) = -2 + 6 + 0 = 4. Now multiply row 2 of matrix 1 by column 1 of matrix 2. -2 · (0) + 1 · 1 + (-6) · 3 = 0 + 1 - 18 = -17. Continue in the same pattern until all the rows of the first matrix have been multiplied by all the rows of the second matrix.

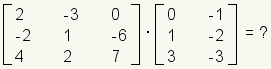
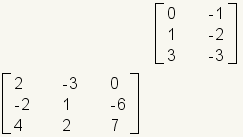
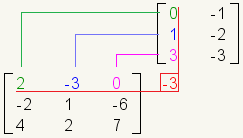
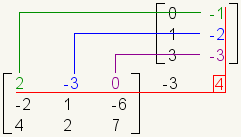
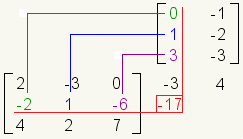
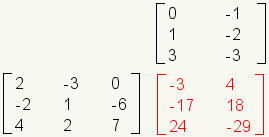
This is how the problem look laid out horizontally:

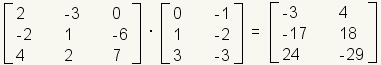
References

1. McAdams, David E.. All Math Words Dictionary, matrix. 2nd Classroom edition 20150108-4799968. pg 114. Life is a Story Problem LLC. January 8, 2015. Buy the book

More Information

• McAdams, David E.. Determinant of a Matrix. allmathwords.org. All Math Words Encyclopedia. Life is a Story Problem LLC. 3/12/2009. https://www.allmathwords.org/en/d/determinant.html.

Educator Resources

• Wired For Space (arrays). NASA LaRC Office of Education. 2/18/2010. http://www.archive.org/details/NasaConnect-WiredForSpace/index.htm.

Cite this article as:

McAdams, David E. Matrix. 4/25/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/m/matrix.html.

Image Credits

• All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Revision History

4/25/2019: Changed equations and expressions to new format. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
9/2/2018: Removed broken links, updated license, implemented new markup. (McAdams, David E.)
8/7/2018: Changed vocabulary links to WORDLINK format. (McAdams, David E.)
3/30/2011: Added information on columns and rows. (McAdams, David E.)
9/28/2009: Minor wording changes to improve readability. (McAdams, David E.)
12/3/2008: Added 'More Information', link to Determinant. (McAdams, David E.)
11/17/2008: Added matrix multiplication. (McAdams, David E.)
3/10/2008: Initial version. (McAdams, David E.)