Doubling Time

Pronunciation: /ˈdʌ.blɪŋ taɪm/ Explain

Click on the blue points on the sliders and drag them to change the figure.

How does the doubling time change when a changes? Why? How does the doubling time change when b changes? Why?
Manipulative 1 - Doubling Time Created with GeoGebra.

Doubling time is the amount of time it takes for an exponential function to double. If an exponential function goes from 1 to 2 in 10 seconds, it will go from 2 to 4 in 10 seconds and 4 to 8 in 10 seconds. An exponential function always doubles in the same amount of time. Manipulative 1 illustrates doubling time for an exponential function of the form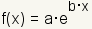

f(x)=a*e^(b*x).

Discovery

  1. How does the doubling time change when a changes? Why?
  2. How does the doubling time change when b changes? Why?

Rule of 72

The rule of 72 can be used to approximate doubling time of investments at a given interest rate. The rule of 72 states: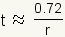
t=0.72/r
where r is the interest rate.

How to Calculate Doubling Time

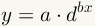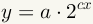Doubling time can be calculated given any exponential equation in the form y=a*d^(b*x). Given this equation, there exists an equation of the form y=a*2^(c*x) that is equivalent to y=a*d^(b*x). Since the base of the second equation is 2, it doubles every time c increases by 1. So c is the doubling time.

StepEquationDescription
1a*d^(bx)=a*2^(cx) Since y = y, the right hand sides of the two equations are equal to each other.
2d^(bx)=2^(cx) Divide both sides by a, eliminating it from the equation. A consequence of this step is that a != 0.
3log base d(2^(cx))=bx Use the definition of logarithm to transform the equation.
4cx*log base d(2)=bx Use the power rule of logarithms to pull cx out of the logarithm.
5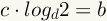c*log base d(2)=b Divide both sides by x, eliminating it from the equation. A consequence of this step is that x != 0.
6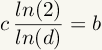c*ln(2)/ln(d)=b Transform the log base d to the natural log using the change of base formula.
7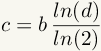c=b*ln(d)/ln(2) Divide both sides by the logarithmic ratio. c is now on one side of the equation by itself. What is on the right hand side of the equation is the doubling time.
Table 1: Derivation of doubling time.

References

  1. McAdams, David E.. All Math Words Dictionary, doubling time. 2nd Classroom edition 20150108-4799968. pg 67. Life is a Story Problem LLC. January 8, 2015. Buy the book
  2. Rule of 72. investopedia.com. Investopedia. Forbes Digital. Last Accessed 7/3/2018. http://investopedia.com/terms/r/ruleof72.asp.
  3. Lodge, Sir Oliver. Easy Mathematics; or, Arithmetic and Algebra for General Readers. pp 353-356. www.archive.org. Macmillan and Company. 1910. Last Accessed 7/3/2018. http://www.archive.org/stream/easymathematicso00lodguoft#page/353/mode/1up. Buy the book
  4. Math 120 Book. pp 698-699. www.archive.org. Last Accessed 7/3/2018. http://www.archive.org/stream/Math120Book-Entire/Math120-fullBook#page/n334/mode/1up/search/doubling.

Cite this article as:

 McAdams, David E. Doubling Time. 4/20/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/d/doublingtime.html.

Image Credits

Revision History

4/20/2019: Updated equations and expressions to the new format (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
7/4/2018: Removed broken links, updated license, implemented new markup, implemented new Geogebra protocol. (McAdams, David E.)
12/16/2008: Initial version. (McAdams, David E.)

All Math Words Encyclopedia is a service of Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License