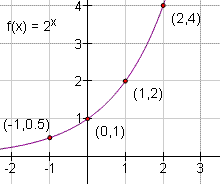Exponential Function

Pronunciation: /ˌɛks.poʊˈnɛn.ʃəl ˈfʌŋk.ʃən/ Explain
Click on the points on the sliders and drag them to change the figure.

Why is the y-intercept always equal to b?
Manipulative 1 - Exponential Function Created with GeoGebra.

An exponential function is a function where the independent variable is an exponent.[3]

The general form for an exponential function is y = b · ax where a and b are constants. b can be considered the initial value. This is because, when x = 0, ax = 1, so b · ax = b. The value of a determines the rate of growth or decay.

Exponential functions where a > 1 are exponential growth functions. This is because the value of the function always increases. Exponential functions where a < 1 are called exponential decay functions because the value of the function always decreases.

Download the Exponential Function Worksheet that goes with this page.

Exponential Growth Functions

Graph of y=1*2^x with the points (0,1), (1,2), (2,4), and (3,8) plotted on the curve.
Figure 1: Graph of f(x) = 1·2x.

Exponential growth functions are so called because the value of an exponential growth function always increases. Exponential growth functions are used to model population growth. An exponential function can accurately model population growth where availability of resources does not overly limit the growth.

One attribute of exponential growth functions is that the value doubles for some time period. In figure 1, the value of the function doubles between x = 0 and x = 1. It doubles again between x = 1 and x = 2. Every time x increases by 1, the value of the function doubles. The time it takes to double is called the doubling time. For the function f(x) = 1·2x in figure 1, the doubling time is 1.

Exponential Decay Functions

Graph with the point (0,2), (1,1), (2,1/2) and the function f(x)=2*(1/2)^x plotted with labels.
Figure 2: Graph of f(x) = 2·(1/2)^x.

Exponential decay functions are so called because the value of an exponential decay function always decreases. Exponential decay functions are used to model radioactive decay and to model how a drug in the body is used up. One form of a exponential decay function is called a half-life function. This is useful for describing a decay function explicitly in terms of the half-life.

How to Graph Exponential Functions

Table 1 gives step by step instructions for graphing the exponential function y = 2·(1/2)x. This can be generalized for any exponential equation in the form y = b · ax.

StepGraphDescription
1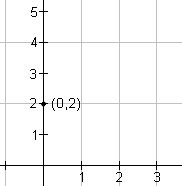Graph with the point (0,2) plotted

Plot the point (0, b). For this equation, plot (0, 2).

2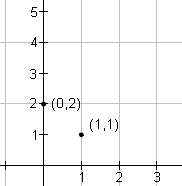Graph with the points (0,2) and (1,1) plotted

Multiply b · a. This gives the value of the function for x = 1. Plot (x, a · b). For this function 2 · (1/2) = 1, so plot (1, 1).

3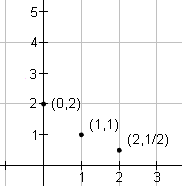Graph with the points (0,2), (1,1), (2,1/2) plotted

Plot the point (2, b · a2). Multiply the y value from step 2 by a. This gives the value for x = 2. For this function, 1 · (1/2) = 1/2, so plot (2, 1/2).

4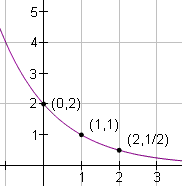Graph with the point (0,2), (1,1), (2,1/2) and the function f(x)=2*(1/2)^x plotted.

Now draw a smooth exponential curve that connects the plotted points. This curve is the graph of the function f(x) = 2 · (1/2)x.

5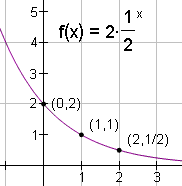Graph with the point (0,2), (1,1), (2,1/2) and the function f(x)=2*(1/2)^x plotted with labels.

Label the graph.

Table 1: Graphing Exponential Functions

References

  1. McAdams, David E.. All Math Words Dictionary, exponential function. 2nd Classroom edition 20150108-4799968. pg 76. Life is a Story Problem LLC. January 8, 2015. Buy the book
  2. exponential function. merriam-webster.com. Encyclopedia Britannica. Merriam-Webster. Last Accessed 7/9/2018. http://www.merriam-webster.com/dictionary/exponential function. Buy the book
  3. Fine, Henry B., Ph. D.. Number-System of Algebra Treated Theoretically and Historically. 2nd edition. pg 44. www.archive.org. D. C. Heath & Co., Boston, U.S.A.. 1907. Last Accessed 7/9/2018. http://www.archive.org/stream/thenumbersystemo17920gut/17920-pdf#page/n53/mode/1up/search/exponential. Buy the book
  4. Metzler, W. H.; Roe, Edward Drake Jr.; Bullard, Warren G.. College algebra. pp 231-241. www.archive.org. Longmans, Green & Co.. 1908. Last Accessed 7/9/2018. http://www.archive.org/stream/collegealgebra00metzrich#page/231/mode/1up/search/exponential+function. Buy the book
  5. Barnard, S. and Child, J. M.. Higher Algebra. revised edition. pp 307-314. www.archive.org. Macmillan & Co Ltd. 1959. Last Accessed 7/9/2018. http://www.archive.org/stream/higheralgebra032813mbp#page/n318/mode/1up/search/exponential+function. Buy the book

More Information

  • McAdams, David E.. Decay. allmathwords.org. All Math Words Encyclopedia. Life is a Story Problem LLC. 3/12/2009. https://www.allmathwords.org/en/d/decay.html.

Cite this article as:

 McAdams, David E. Exponential Function. 4/20/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/e/exponentialfunction.html.

Image Credits

Revision History

4/20/2019: Updated expressions and equations to match new format. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
7/5/2018: Removed broken links, updated license, implemented new markup, implemented new Geogebra protocol. (McAdams, David E.)
2/2/2010: Added "References". (McAdams, David E.)
12/19/2009: Added "References". (McAdams, David E.)
8/1/2008: Added manipulative 1. Added vocabulary links for 'decay' and 'growth' (McAdams, David E.)
5/10/2008: Initial version. (McAdams, David E.)

All Math Words Encyclopedia is a service of Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License