Equilateral Triangle

Pronunciation: /ˌi.kwəˈlæ.tər.əl ˈtraɪˌæŋ.gəl/ Explain

The sides of this triangle are always the same length, are equilateral.

Manipulative 1 - Equilateral Triangle Created with GeoGebra.

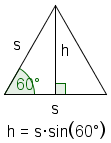
An equilateral triangle is a triangle where all of the sides are the same length.^[3]

Properties of an Equilateral Triangle

Property

Equation

Description

Length of the sides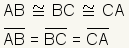

length of AB = length of BC = length of CA.

The length of the sides of an equilateral triangle are equal by definition. The length of a side of an equilateral triangle is conventionally represented by the variable s.

Angles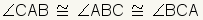

angle CAB is congruent with angle ABC and both are congruent with angle BCA

The angles of an equilateral triangle are congruent.

Measure of the angles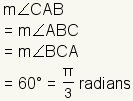

measure of angle CAB = measure of angle ABC = measure of angle BCA = 60 degrees = pi/3 radians.

The angles of an equilateral triangle all measure 60° or π/3 radians

Altitude

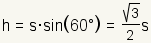h = s*sin(60°) = s*((square root of 3)/2)

Equilateral triangle showing the calculation of height as h=s*sin(60).

The altitude of an equilateral triangle is h = s·sin(60°).

Area

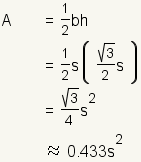$A = (1/2)bh = \(1/2)s*(s*sin(60°)) = (s^2*square root of 3)/4 which is approximately 0.433*s^2$

The area of an equilateral triangle is 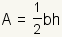A=(1/2)bh

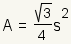. Using the formula for the altitude, A=s^2*(square root of 3)/4.

Inradius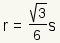

The inradius of an equilateral triangle is 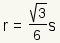r=(square root of 6)/6*s

Circumradius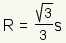

The circumradius of an equilateral triangle is 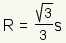R=(square root of 3)/3*s

Area of the incircle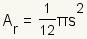

The area of the incircle of an equilateral triangle is 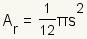Ar=(1/12)pi*s^2

Area of the circumcircle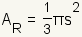

The area of the circumcircle of an equilateral triangle is 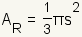Ar=(1/3)pi*s^2

Table 1

Constructing an Equilateral Triangle

Step	Example	Description	Justification
1		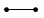Start with a line segment
2		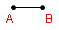Label the end points `A` and `B`.
3		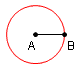Construct a circle with the center at `A` and the radius the length of segment `AB`.	Euclid's Elements Book 1 Postulate 3: A circle can be drawn with any center and any radius.
4		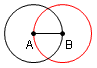Construct a circle with the center at `B` and the radius the length of segment `AB`.	Euclid's Elements Book 1 Postulate 3: A circle can be drawn with any center and any radius.
5		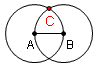Label an intersection of the two circles `C`.
6		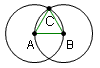Construct a line segment `AC` and `BC`. This forms triangle `ABC`.	Euclid's Elements Book 1 Postulate 1: A straight line can be drawn from any point to any point.
7		Since they are radii of the same circle, the line segment `AC` is the same length as the line segment `AB`. Similarly, the line segment `BC` is the same length as the line segment `AB`.	Euclid's Elements Book 1 Definition 15: A circle is all points equidistant from a center point.
8		Since `AB` ≡ `AC` and `AB` ≡ `BC`, then it must be true that `AC` ≡ `BC`.	Euclid's Elements Book 1 Common Notion 1: If A = B and B = C then A = C.
9		By the definition of an equilateral triangle, the triangle `ABC` is equilateral.	Euclid's Elements Book 1 Definition 20: An equilateral triangle is a triangle where the length of all three sides is the same.
		Q.E.D.
Table 2

References

McAdams, David E.. All Math Words Dictionary, equilateral triangle. 2nd Classroom edition 20150108-4799968. pg 71. Life is a Story Problem LLC. January 8, 2015. Buy the book
equilateral triangle. merriam-webster.com. Encyclopedia Britannica. Merriam-Webster. Last Accessed 7/9/2018. http://www.merriam-webster.com/dictionary/equilateral triangle. Buy the book
Casey, John, LL.D., F.R.S.. The First Six Books of the Elements of Euclid. pp 8,11-12. Translated by Casey, John, LL.D. F.R.S.. www.archive.org. Hodges, Figgis & Co.. 1890. Last Accessed 7/9/2018. http://www.archive.org/stream/firstsixbooksofe00caseuoft#page/8/mode/1up/search/equilateral. Buy the book
Le Clerc, Sébastien; Nattes, John Claude; Pyne, W. H.. Nattes's practical geometry, or, Introduction to perspective. pg 11. www.archive.org. W. Miller. 1805. Last Accessed 7/9/2018. http://www.archive.org/stream/nattesspractical00leclrich#page/11/mode/1up/search/equilateral. Buy the book

More Information

Euclid. Elements Book 1, Proposition 1: To construct an equilateral triangle on a given finite straight line.. mathcs.clarku.edu. 3/12/2009. https://mathcs.clarku.edu/~djoyce/elements/bookI/propI1.html.
Euclid of Alexandria. Elements. mathcs.clarku.edu. Clark University. 9/6/2018. https://mathcs.clarku.edu/~djoyce/elements/elements.html.

Cite this article as:

McAdams, David E. Equilateral Triangle. 4/20/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/e/equilateraltriangle.html.

Image Credits

All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Revision History

4/20/2019: Updated expressions and equations to match new format. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
7/5/2018: Removed broken links, updated license, implemented new markup, implemented new Geogebra protocol. (McAdams, David E.)
1/26/2010: Added "References". (McAdams, David E.)
12/18/2008: Added 'Properties of an Equilateral Triangle' and changed figure to manipulative. (McAdams, David E.)
8/20/2007: Added construction of an equilateral triangle. (McAdams, David E.)
7/12/2007: Initial version. (McAdams, David E.)

#	A	B	C	D
E	F	G	H	I
J	K	L	M	N
O	P	Q	R	S
T	U	V	W	X
Y	Z

All Math Words Encyclopedia is a service of Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License