Angle
Pronunciation: /ˈæŋ.gəl/ ExplainAn angle is the rotation between two intersecting lines, ray or line segments.
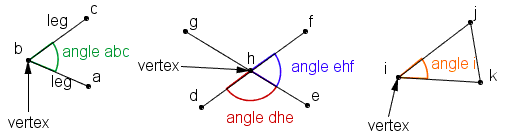 |
| Figure 1: Various angles |
The vertex of an angle is the point of intersection of the lines. In figure 1, the vertices are the points b, h, and i. The legs, also called sides, of an angle are the lines, rays, or line segments that define the angle.
Two angles are equiangular if the measures of the angles are the same.
Article Index
Measure of an Angle
The measure of an angle is made in terms of the measure of a full circle. The unit of measure for an angle is degrees, radians or, in rare cases, gradians.
Degree
|
One degree is 1/360 of a circle.
Degree is the oldest unit of measure for
an angle. Degrees are denoted by a small circle (°) or
the abbreviation deg. By definition, a full
circle is 360°. This means that an angle that is 1/4 of a circle
is 360°/4, or 90°. See manipulative 1.
|
Radian
|
When measuring angles, the radian is
particularly useful. A radian is defined as the angle made with an
arc length of 1 on a
unit circle.
This means that the length of an arc of 1 radian is the same as the length of
the radius of the circle. See manipulative 2. There are
2π
radians in a full circle. An angle that is 1/5 of a circle is
2π/5 ≈ 1.26 radians. The abbreviation for radian is
rad.
One reason the measure of radians is so useful has to do with Euler's famous equation that relates exponentiation with trigonometry using complex numbers: eiθ = cos(θ) + i·sin(θ). This equation only works if the angle θ is measured in radians.
|
Gradian
A rarely used angle measure is gradians. A full circle measures 400 gradians. The abbreviation for gradians is grad.
Classes of Angles
|
For convenience in discussions of angles and trigonometry, angles are divided into classes. The class an angle belongs to is determined by its measure. Table 1 shows the classes of angles and their measures. Manipulative 3 also shows the classes of angles and their measures.
| ||||||||||||||||||||||||||||||||||
Inscribed Angle
|
An inscribed angle is an angle drawn inside a
circle.
Discovery
|
Central Angle
|
A central angle of a circle is an angle with the vertex at the center of the circle and the other two points on the circumference of the circle. For an inscribed angle and a central angle with the same endpoints, the measure of the inscribed angle is half the measure of the central angle. |
|
Angle of Rotation
|
An Angle of Rotation is the amount of rotation about a center of rotation. |
Complementary Angles
|
Two angles are complementary if they produce a
right angle
when combined. This means that given angles α and
β, α and
β are complementary if
α + β = π/2.
Supplementary Angles
|
|
Copying an Angle
An angle can be copied using a compass and a straight edge.|
Click on the blue points and drag them to change the figure. Click on the Step slider and drag it to see each step. Review the steps for copying an angle, then try it on a piece of paper. |
| Manipulative 10 - How to Copy an Angle Created with GeoGebra. |
Angle Bisector
| An angle bisector is a line segment or ray that divides an angle into two congruent angles. For details on how to bisect an angle, see How to Bisect an Angle. |
Angle Addition Postulate
|
Click on the blue points and drag them to change the figure. What is the relationship between the three angles? |
| Manipulative 12 - Angle Addition Postulate Created with GeoGebra. |
The angle addition postulate states that adjacent angles can be added together to form a larger angle. This is a postulate or axiom, meaning it is accepted as true without proof. The exact mathematical definition of the Angle Addition Postulate is:
Given non-collinear points A, B, C and a point D in the interior of ∠BAC, m∠BAD + m∠DAC = m∠BAC.
Table of Figures
- Various angles
- 90 degree angle
- 1 radian
- Inscribed angles
- An angle inscribed in a circle
- An angle inscribed in the diameter of a circle
- Central angle of a circle.
- Relationship between central and inscribed angles
- Complementary Angles
- Supplementary Angles
- Copying an Angle
- Angle Bisector
- Bisecting an Angle
References
- McAdams, David E.. All Math Words Dictionary, angle. 2nd Classroom edition 20150108-4799968. pg 15. Life is a Story Problem LLC. January 8, 2015. Buy the book
Educator Resources
- Angles and Direction Experiment . NASA LaRC Office of Education. 2/18/2010. http://www.archive.org/details/NasaConnect-Wygtya-AnglesAndDirectionExperiment/index.htm.
- Angle Activity. NASA LaRC Office of Education. 2/18/2010. http://www.archive.org/details/NasaConnect-Eom-AngleActivity/index.htm.
- Geometry of Exploration - Eyes Over Mars. NASA LaRC Office of Education. 2/18/2010. http://www.archive.org/details/NasaConnect-GeometryOfExploration-EyesOverMars/index.htm.
Cite this article as:
McAdams, David E. Angle. 4/12/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/a/angle.html.Image Credits
- All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Revision History
4/12/2019: Changed equations and expressions to new format. (McAdams, David E.)12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
8/28/2018: Corrected spelling. (McAdams, David E.)
6/14/2018: Removed broken links, changed Geogebra links to work with Geogebra 5, updated license, implemented new markup. (McAdams, David E.)
12/26/2009: Added "References". (McAdams, David E.)
10/28/2008: Changed manipulatives and some graphics to geogebra. (McAdams, David E.)
9/19/2008: Changed heading 'Other Information' to 'More Information', dictionary.com to more information (McAdams, David E.)
7/7/2008: Corrected link errors. (McAdams, David E.)
4/28/2008: Added keyword class to angle classifications. (McAdams, David E.)
4/19/2008: Revised bisecting an angle table to reflect most common method. (McAdams, David E.)
3/11/2008: Fixed various formatting and link errors. (McAdams, David E.)
2/3/2008: Changed HTML entity angle to the word angle. (McAdams, David E.)
8/17/2007: Initial version. (McAdams, David E.)
- Navigation
- Home
- Contents
-
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z - Teacher Aids
- Classroom Demos
- How To
- LIASP
- LIASP Home
- Conditions of Use
- Privacy Policy
- Donate to LIASP
- Help build this site
- About LIASP
- Contact LIASP
All Math Words Encyclopedia is a service of
Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License

 Understanding Check
Understanding Check