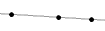Collinear
Pronunciation: /koʊˈlɪn.i.ər/ Explain
|
If points are collinear, they are in the same line[2][3]. Since two points define a line, any two points are collinear (see figure 1). If three points are collinear, a line drawn using any two of the points will contain the third (see figure 2). If objects are non-collinear, no one line can be drawn that contains all the objects (see figure 3). |
|
Related Words
Collinearity: Having to do with whether or not objects are in the same line.
How to tell if Points are Collinear
|
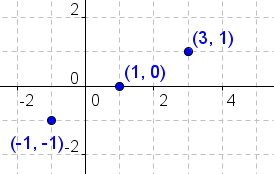
In 2-dimensional analytical geometry, each point has an x-coordinate and a y-coordinate. These coordinates can be used to see if three are collinear. To see if three or more points are collinear, pick one of the points as a reference point. If the slopes of the lines defined by the reference point and each of the other points are equal, the points are collinear. Table 1 shows the steps for determining if the points in figure 3 are collinear. |
| Step | Equation(s) | Discussion |
|---|---|---|
| 1 | 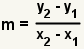 |
This algorithm starts with the equation of a line in point slope form. |
| 2 | 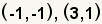 |
Start by selecting any two of the points. For this demonstration, select (-1,-1) and (3,1). |
| 3 | 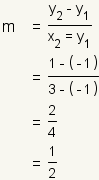 |
Use the slope formula to determine the slope of the line defined by the two points. |
| 4 |  |
Now pick one of the points already used and the third point. |
| 5 | 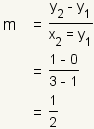 |
Find the slope of the line defined by those two points. |
| 6 | 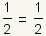 |
Since the slopes are equal, the three points are collinear. |
| Table 1: How to find out if three points are collinear. | ||
References
- McAdams, David E.. All Math Words Dictionary, collinear. 2nd Classroom edition 20150108-4799968. pg 36. Life is a Story Problem LLC. January 8, 2015. Buy the book
- Casey, John, LL.D., F.R.S.. The First Six Books of the Elements of Euclid. pg 5. Translated by Casey, John, LL.D. F.R.S.. www.archive.org. Hodges, Figgis & Co.. 1890. Last Accessed 6/25/2018. http://www.archive.org/stream/firstsixbooksofe00caseuoft#page/5/mode/1up/search/collinear. Buy the book
- Palmer, Claude Erwin and Taylor, Daniel Pomeroy. Solid Geometry. pg 280. www.archive.org. Scott, Foresman and Company. 1918. Last Accessed 6/25/2018. http://www.archive.org/stream/solidgeometry00palmrich#page/280/mode/1up/search/collinear. Buy the book
Cite this article as:
McAdams, David E. Collinear. 4/13/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/c/collinear.html.Image Credits
- All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Revision History
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)6/25/2018: Removed broken links, updated license, implemented new markup, updated GeoGebra apps. (McAdams, David E.)
3/15/2010: Improved instructions for manipulative 3. Added section on analytical geometry. (McAdams, David E.)
1/12/2010: Added "References". (McAdams, David E.)
7/5/2008: Added More Information. (McAdams, David E.)
8/23/2007: Initial version. (McAdams, David E.)
- Navigation
- Home
- Contents
-
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z - Teacher Aids
- Classroom Demos
- How To
- LIASP
- LIASP Home
- Conditions of Use
- Privacy Policy
- Donate to LIASP
- Help build this site
- About LIASP
- Contact LIASP
All Math Words Encyclopedia is a service of
Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License