Factorial

Pronunciation: /fækˈtoʊr.i.əl/ Explain

A factorial of n is the product of all integers from 1 to n, inclusive. The exclamation mark (!) is the unary operator that represents factorial. The expression '5!' is read, "Five factorial" and means 1·2·3·4·5 which equals 120. Zero factorial (0!) is treated as a special case and is defined to be 0! = 1. At this level of mathematics, the n in n! must be a non-negative integer.

In advanced mathematics, factorial is defined using the gamma function:

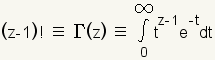Equation 1

First 11 Factorials

Table of Factorials

n	Formula	n!
0	None	1
1	1! = 1	1
2	2! = 1·2	2
3	3! = 1·2·3	6
4	4! = 1·2·3·4	24
5	5! = 1·2·3·4·5	120
6	6! = 1·2·3·4·5·6	720
7	7! = 1·2·3·4·5·6·7	5040
8	8! = 1·2·3·4·5·6·7·8	40,320
9	9! = 1·2·3·4·5·6·7·8·9	362,880
10	10! = 1·2·3·4·5·6·7·8·9·10	3,628,800
Table 1

Working With Factorials

Since factorials get very large very quickly (see table 1), they can be difficult to calculate without a calculator. However, when used in mathematics, equations using factorials usually involve ratios of factorials. Since factorials by definition have many common factors, these problems can be reduced in difficulty by canceling common factors.

To understand this, start with the definition of a combination:

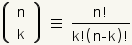Equation 1

If one wishes to calculate 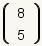, the formula is: .

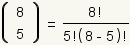First, write out the factorials: .

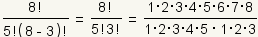Now use the property of multiplying by 1 to cancel all ones: .

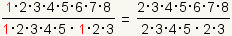Now cancel the factors that are the same: .

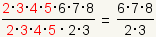Now look for remaining factors that have common factors. In the case, 2·3 = 6 so the 6 on the top cancels the 2·3 on the bottom: .

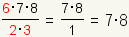This has now become a simple multiplication problem. Since 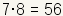, there are exactly 56 ways that five objects selected from a pool of eight objects can be arranged. So, .

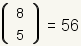References

1. McAdams, David E.. All Math Words Dictionary, factorial. 2nd Classroom edition 20150108-4799968. pg 78. Life is a Story Problem LLC. January 8, 2015. Buy the book
2. Bettinger, Alvin K. and Englund John A.. Algebra And Trigonometry. pg 97. www.archive.org. International Textbook Company. January 1963. Last Accessed 7/11/2018. http://www.archive.org/stream/algebraandtrigon033520mbp#page/n114/mode/1up/search/factorial. Buy the book
3. Aley, Robert J. and Rothrock, David A.. The Essentials of Algebra for Secondary Schools. pg 272. www.archive.org. Silver, Burdett and Company. 1904. Last Accessed 7/11/2018. http://www.archive.org/stream/cu31924031286143#page/n283/mode/1up/search/factorial. Buy the book
4. Lodge, Sir Oliver. Easy Mathematics; or, Arithmetic and Algebra for General Readers. pp 315-317. www.archive.org. Macmillan and Company, Limited. 1910. Last Accessed 7/11/2018. http://www.archive.org/stream/easymathematicso00lodguoft#page/315/mode/1up/search/factorial. Buy the book

More Information

• (some) factorials from 1 to 100,000:. gutenberg.org. 12/19/2009. http://www.gutenberg.org/dirs/etext95/factr10.txt.

Cite this article as:

McAdams, David E. Factorial. 4/21/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/f/factorial.html.

Image Credits

• All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Revision History

4/21/2019: Modified equations and expression to match the new format. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
7/9/2018: Removed broken links, updated license, implemented new markup, implemented new Geogebra protocol. (McAdams, David E.)
2/4/2010: Added "References". (McAdams, David E.)
12/29/2008: Corrected equations. (McAdams, David E.)
4/23/2008: Initial version. (McAdams, David E.)