Identity

Pronunciation: /aɪˈdɛn.tɪ.ti/ Explain

1. An identity is a value and an operation such that applying the value and operation does not change the result.

   The additive identity for real numbers is 0. This is because one can add 0 to any value, and the result is the same. Example: 3 + 0 = 3.

   The multiplicative identity for real numbers is 1. This is because one can multiply any value by 1, and the result is the original value. Example: -5 · 1 = -5.

   Identity	Description
   a + 0 = a	The additive identity for real numbers is the number 0. This is because, for any real number a, a + 0 = a.
   a · 1 = a	The multiplicative identity for real numbers is 1. You can see that a · 1 = a.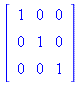
   	The identity for a square matrix under multiplication is a diagonal matrix where every diagonal value is 1.

2. An identity is an equation that is true for all values of the variables used in the equation. One example of an identity is the equation sin(x)²+cos(x)² = 1. This identity is always true for any value of x. An identity can be used to solve equations or find the derivative of equations by transforming an equation into a more useful form:

   Equation	Description
   sin(x)2 + sin(x) = 1 - cos(x)2	Equation to solve.
   sin(x)2 + cos(x)2 + sin(x) = 1	Add cos(x)2 to both sides of the equations.
   1 + sin(x) = 1	Substitute 1 for sin(x)2 + cos(x)2.
   sin(x) = 0	Subtract 1 from both sides.
   x ∈ {0, π, 2π, 3π, ...}	Transform equation from trigonometric form to set form.
   Table 1: Using an identity to solve an equation.

References

1. McAdams, David E.. All Math Words Dictionary, identity. 2nd Classroom edition 20150108-4799968. pg 93-94. Life is a Story Problem LLC. January 8, 2015. Buy the book
2. Bettinger, Alvin K. and Englund, John A.. Algebra and Trigonometry. pg 17. www.archive.org. International Textbook Company. January 1963. Last Accessed 8/7/2018. http://www.archive.org/stream/algebraandtrigon033520mbp#page/n18/mode/1up. Buy the book
3. Gilbert, Jimmie; and Gilbert Linda. Elements of Modern Algebra. 6th edition. pp 29-30. Thomson, Brooks/Cole. 2005. Last Accessed 8/7/2018. Buy the book
4. Mary Jane Sterling. Algebra II For Dummies. pg 12. For Dummies. June 19, 2006. Last Accessed 8/7/2018. Buy the book

More Information

• McAdams, David E.. Additive Identity. allmathwords.org. All Math Words Encyclopedia. Life is a Story Problem LLC. 2/11/2010. https://www.allmathwords.org/en/a/additiveidentity.html.

Cite this article as:

McAdams, David E. Identity. 4/23/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/i/identity.html.

Image Credits

• All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Revision History

4/23/2019: Updated equations and expressions to new format. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
8/6/2018: Removed broken links, updated license, implemented new markup, implemented new Geogebra protocol. (McAdams, David E.)
2/11/2010: Added "References". (McAdams, David E.)
8/9/2008: Added More Information, definition 2. (McAdams, David E.)
7/12/2007: Initial version. (McAdams, David E.)