Menelaus’s Theorem
Pronunciation: /ˌmɛn.ɪˈleɪ.əs ˈθɪər.əm/ Explain|
Menelaus’s theorem relates the way two cevians of a triangle divide each other and the sides of a triangle. Menelaus’s theorem is named for Menelaus of Alexandria. Stated mathematically, Menelaus's theorem claims that, given
triangle
ABC, and a
transversal
line that crosses the extended sides of
BC, AC, and AB at points D,
E, and F respectively, with D, E,
and F distinct from A, B, and C, then
|
| ||
|
It is important to know that this theorem uses signed lengths of segments. Any segment that goes from left to right is positive. Any segment that goes from right to left is negative. Maniplulative 2 demonstrates positive and negative line segments. |
|
References
- McAdams, David E.. All Math Words Dictionary, menelaus’s theorem. 2nd Classroom edition 20150108-4799968. pg 116. Life is a Story Problem LLC. January 8, 2015. Buy the book
Cite this article as:
McAdams, David E. Menelaus’s Theorem. 4/25/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/m/menelaustheorem.html.Image Credits
- All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Revision History
4/25/2019: Changed equations and expressions to new format. (McAdams, David E.)12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
9/3/2018: Removed broken links, updated license, implemented new markup. (McAdams, David E.)
7/18/2018: Changed title to common format. (McAdams, David E.)
5/5/2011: Initial version. (McAdams, David E.)
- Navigation
- Home
- Contents
-
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z - Teacher Aids
- Classroom Demos
- How To
- LIASP
- LIASP Home
- Conditions of Use
- Privacy Policy
- Donate to LIASP
- Help build this site
- About LIASP
- Contact LIASP
All Math Words Encyclopedia is a service of
Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License
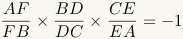 Or, stated another way:
Or, stated another way:
