Transversal

Pronunciation: /trænzˈvɜr.səl/ Explain

Click on the blue points and drag them to change the figure. Manipulative 1 - Transversal of Two Lines Created with GeoGebra.

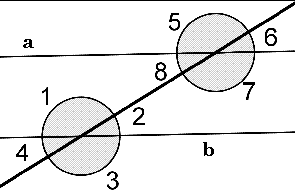
A transversal is a line that intersects two other possibly parallel lines. Transversal are important in geometry because the theorems based on the relationships of angles formed by a transversal are used in many other theorems. The line that intersects the two other lines is called the transversal. The lines that are crossed are called the transversed lines. The various pairs of angles in a transversal are named to make it easier to describe the relationships.

Figure 2: Transversal

Names of angles in a transversal Name Description Angle numbers Exterior Exterior angles are on the outside of the transversed lines. Angles 3, 4, 5 and 6 are exterior angles. Interior Interior angles are between the transversed lines. Angles 1, 2, 7 and 8 are interior angles Alternate Alternate angles are on opposite sides the transversal. Angles 1, 4, 5, and 8 are alternate to 2, 3, 6 and 7. Consecutive Consecutive angles are adjacent angles on the same side of the transversal. Angle pairs 1 and 8, 2 and 7 are consecutive. Corresponding Corresponding angles are angles that are in the same positions relative to the two intersections. Angle pairs 1 and 5, 2 and 6, 3 and 7, 4 and 8 are corresponding angles. Vertical Vertical angles are opposite each other at an intersection. Angle pairs 1 and 3, 2 and 4, 5 and 7, 6 and 8 are vertical angles. Alternate interior Angle pairs that are interior angles and are opposite each other. Angle pairs 1 and 7, 2 and 8 are alternate interior angles. Alternate exterior Angle pairs that are exterior angles and are opposite each other. Angle pairs 3 and 5, 4 and 6 are alternate exterior angles. Table 1: Names of angles in a transversal

Postulates and Theorems

There are a number of postulates and theorems associated with transversals of parallel lines:

• Corresponding Angles Congruence Postulate: Corresponding angles of a transversal of parallel lines are congruent.
• Alternate Exterior Angles Congruence Theorem: Alternate exterior angles of a transversal of parallel lines are congruent.
• Alternate Interior Angles Congruence Theorem: Alternate interior angles of a transversal of parallel lines are congruent.
• Consecutive Interior Angles Supplement Theorem: Consecutive interior angles of a transversal of parallel lines are supplementary.
• Corresponding Angles Congruence Converse Theorem: If any pair of corresponding angles of a transversal are congruent, then the transversed lines are parallel.
• Alternate Exterior Angles Converse Theorem: If any pair of alternate exterior angles of a transversal are congruent, then the transversed lines are parallel.
• Alternate Interior Angles Converse Theorem: If any pair of alternate interior angles of a transversal are congruent, then the transversed lines are parallel.
• Consecutive Interior Angles Supplement Converse Theorem: If any pair of consecutive interior angles of a transversal are supplementary, then the transversed lines are parallel.

References

1. McAdams, David E.. All Math Words Dictionary, transversal. 2nd Classroom edition 20150108-4799968. pg 181. Life is a Story Problem LLC. January 8, 2015. Buy the book

More Information

• McAdams, David E.. Alternate angles. allmathwords.org. All Math Words Encyclopedia. Life is a Story Problem LLC. 10/13/2010. https://www.allmathwords.org/en/a/alternateangles.html.

Cite this article as:

McAdams, David E. Transversal. 1/17/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/t/transversal.html.

Image Credits

• All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Revision History

12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
12/14/2018: Removed broken links, updated license, implemented new markup. Changed geogebra to new format. (McAdams, David E.)
8/7/2018: Changed vocabulary links to WORDLINK format. (McAdams, David E.)
5/5/2011: Initial version. (McAdams, David E.)