Pentagon
Pronunciation: /ˈpɛntəˌgɒn/ Explain
|
A pentagon is a five-sided polygon. A regular pentagon is a five-sided equilateral polygon. Click on the blue points in manipulatives 1 and 2 and drag them to change the figure. |
|
Properties of a Regular Pengagon
|
|
Tilings of Pentagons

Figure 1: Tiling of a pentagon. Courtesy John Savard. 
Figure 2: Tiling of a pentagon.
Geometric nets that include pentagons
| Example | Name | Printable Net |
|---|---|---|
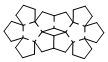 | Dodecahedron | net_dodecahedron.pdf |
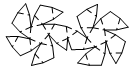 | Icosidodecahedron | net_icosidodecahedron.pdf |
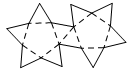 | Pentagonal Antiprism | net_pentagonal_antiprism.pdf |
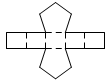 | Pentagonal Prism | net_pentagonal_prism.pdf |
 | Pentagonal Pyramid | net_pentagonal_pyramid.pdf |
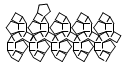 | Rhombidodecahedron | net_rhombidodecahedron.pdf |
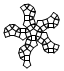 | Rombicosidodecahedron | net_rombicosidodecahedron.pdf |
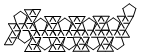 | Snub Dodecahedron | net_snub_dodecahedron.pdf |
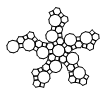 | Truncated Icosidodecahedron | net_trunc_icosidodecahedron.pdf |
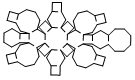 | Truncated Cuboctahedron | net_truncated_cuboctahedron.pdf |
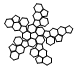 | Truncated Icosahedron | net_truncated_icosahedron.pdf |
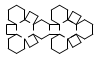 | Truncated Octahedron | net_truncated_octahedron.pdf |
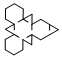 | Truncated Tetrahedron | net_truncated_tetrahedron.pdf |
References
- McAdams, David E.. All Math Words Dictionary, pentagon. 2nd Classroom edition 20150108-4799968. pg 136. Life is a Story Problem LLC. January 8, 2015. Buy the book
- Stöcker, K.H.. The Elements of Constructive Geometry, Inductively Presented. pg 27. Translated by Noetling, William A.M, C.E.. www.archive.org. Silver, Burdett & Company. 1897. Last Accessed 12/3/2018. http://www.archive.org/stream/elementsofconstr00noetrich#page/27/mode/1up. Buy the book
- Casey, John, LL.D., F.R.S.. The First Six Books of the Elements of Euclid. pg 9. Translated by Casey, John, LL.D. F.R.S.. www.archive.org. Hodges, Figgis & Co.. 1890. Last Accessed 12/3/2018. http://www.archive.org/stream/firstsixbooksofe00caseuoft#page/9/mode/1up/search/pentagon. Buy the book
- Keller, Samuel Smith. Mathematics for Engineering Students, Plane and Solid Geometry. pg 9. www.archive.org. D. Van Nostrand Company. 1908. Last Accessed 12/3/2018. http://www.archive.org/stream/firstsixbooksofe00caseuoft#page/9/mode/1up/search/pentagon. Buy the book
More Information
- Wolchover, Natalie. Pentagon Tiling Proof Solves Century-Old Math Problem. https://www.quantamagazine.org. Quanta Magazine. 12/3/2018. https://www.quantamagazine.org/pentagon-tiling-proof-solves-century-old-math-problem-20170711/.
Cite this article as:
McAdams, David E. Pentagon. 12/21/2018. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/p/pentagon.html.Image Credits
- All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Revision History
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)12/1/2018: Removed broken links, updated license, implemented new markup, updated geogebra app. (McAdams, David E.)
8/28/2018: Corrected spelling. (McAdams, David E.)
8/7/2018: Changed vocabulary links to WORDLINK format. (McAdams, David E.)
12/31/2009: Initial version. (McAdams, David E.)
- Navigation
- Home
- Contents
-
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z - Teacher Aids
- Classroom Demos
- How To
- LIASP
- LIASP Home
- Conditions of Use
- Privacy Policy
- Donate to LIASP
- Help build this site
- About LIASP
- Contact LIASP
All Math Words Encyclopedia is a service of
Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License
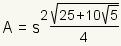 .
.