Polygon
Pronunciation: /ˈpɒl.iˌgɒn/ ExplainA polygon is an n-sided closed figure in a plane. Each of the sides of a polygon is a straight line segment. Since a polygon is closed, each of the line segments is connected to another at both ends. Examples of polygons are triangles, rectangles, and pentagons. An n-sided polygon is called an n-gon.
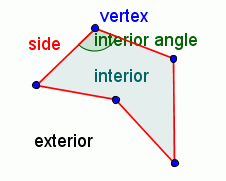
Parts of a polygon
|
|
Properties of polygons
- Straight line segments - The edges of polygons are straight line segments. Each line segment is connected to the other line segments at its endpoints.
- closed - Polygons are closed figures. A pencil placed on one point on the edge of the polygon and traced around the edge will return to the same point without retracing.
- Connected - Polygons are all in one piece.
- concave or convex - A polygon can be concave or convex. A polygon is convex if a line segment drawn between any two points in the polygon remains within the polygon.
- Simple or complex - A polygon can be simple or complex. In a simple polygon, none of the edges cross.
Regular polygon
A regular polygon is a polygon that is simple, convex and equilateral.
Some Types of polygons
| Name | Sides | Illustration | --- Regular ---- | ||||
|---|---|---|---|---|---|---|---|
| Central angle | Internal angle | Inradius/ apothem | Circumradius | Area | |||
| n-gon | n | 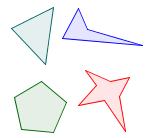 |
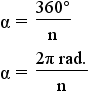 |
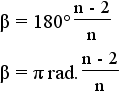 |
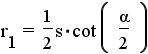 |
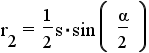 |
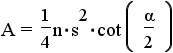 |
| triangle | 3 |  |
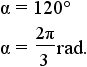 |
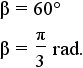 |
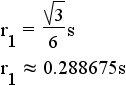 |
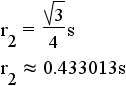 |
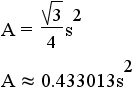 |
| quadrilateral | 4 |  |
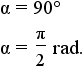 |
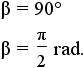 |
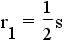 |
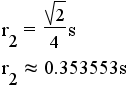 |
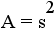 |
| pentagon | 5 |  |
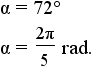 |
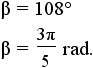 |
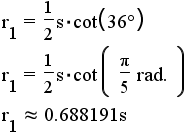 |
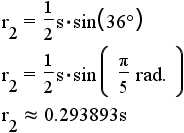 |
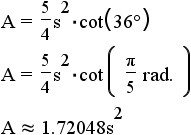 |
| hexagon | 6 |  |
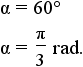 |
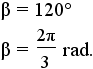 |
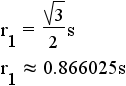 |
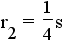 |
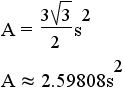 |
| Table 2: Some Types of polygons | |||||||
References
- McAdams, David E.. All Math Words Dictionary, polygon. 2nd Classroom edition 20150108-4799968. pg 141. Life is a Story Problem LLC. January 8, 2015. Buy the book
More Information
- McAdams, David E.. Regular Polygon. allmathwords.org. Life is a Story Problem LLC. 3/12/2009. https://www.allmathwords.org/en/r/regularpolygon.html.
Cite this article as:
McAdams, David E. Polygon. 12/21/2018. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/p/polygon.html.Image Credits
- All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Revision History
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)12/1/2018: Removed broken links, updated license, implemented new markup. (McAdams, David E.)
8/7/2018: Changed vocabulary links to WORDLINK format. (McAdams, David E.)
12/31/2009: Added "References". (McAdams, David E.)
9/3/2008: Expanded 'More Information'. (McAdams, David E.)
7/12/2007: Initial version. (McAdams, David E.)
- Navigation
- Home
- Contents
-
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z - Teacher Aids
- Classroom Demos
- How To
- LIASP
- LIASP Home
- Conditions of Use
- Privacy Policy
- Donate to LIASP
- Help build this site
- About LIASP
- Contact LIASP
All Math Words Encyclopedia is a service of
Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License