Regular Polygon
Pronunciation: /ˈrɛg.jə.lər ˈpɒl.iˌgɒn/ ExplainA regular polygon is a polygon whose sides are equal length and whose sides are symmetrical about the center of the polygon.[2] Regular polygons of various number of sides can be denoted as 'regular n-gon'. A regular 3-gon is also called an equilateral triangle. A regular 4-gon is called a square.
|
Click on the blue points and drag them to change the figure. |
| Manipulative 1 - Regular Polygons Created with GeoGebra. |
Center of Regular Polygons
|
Each regular polygon has a center. This center can be found by constructing the perpendicular bisectors of any two sides of the regular polygon that are not opposite each other. The point of intersection of the perpendicular bisectors is the center of the regular polygon. For polygons with an even number of sides, the center can be found by connecting any two sets of antipodal (opposite) points. |
Central Angle of Regular Polygons
|
The central angle of a regular polygon is the angle between
two rays that go from the center of the regular polygon and pass through two adjacent
vertices of the polygon. The measure of the central angle of regular polygons is
|
Circumcircle About Regular Polygons
|
A circle can be drawn around every regular polygon that intercepts all the vertices of the polygon and none of the sides. This is the circumcircle of the regular polygon. The center of the regular polygon is also the circumcenter of the regular polygon. To construct the circumcircle about a regular polygon, place the point of the compass at the center of the polygon, and the stylus on a vertex, then draw the circle. |
Incircle of Regular Polygons
|
A circle can be drawn inside every regular polygon that intercepts each of the sides of the polygon exactly once. This is the incircle of the regular polygon. The center of the regular polygon is also the incenter of the regular polygon. To construct the incircle of a regular polygon, construct the midpoint of any of the sides. Then place the point of the compass at the center of the polygon, and the stylus on the midpoint, then draw the circle. |
References
- McAdams, David E.. All Math Words Dictionary, regular polygon. 2nd Classroom edition 20150108-4799968. pg 154. Life is a Story Problem LLC. January 8, 2015. Buy the book
- Stöcker, K.H.. The Elements of Constructive Geometry, Inductively Presented. pg 28. Translated by Noetling, William A.M, C.E.. www.archive.org. Silver, Burdett & Company. 1897. Last Accessed 12/4/2018. http://www.archive.org/stream/elementsofconstr00noetrich#page/28/mode/1up. Buy the book
- Convex. ams.org. Geometry Glossary. American Mathematical Society. Last Accessed 12/4/2018. http://www.ams.org/featurecolumn/archive/geometry-glossary.html.
More Information
- McAdams, David E.. Polygon. allmathwords.org. All Math Words Encyclopedia. Life is a Story Problem LLC. 3/12/2009. https://www.allmathwords.org/en/p/polygon.html.
Cite this article as:
McAdams, David E. Regular Polygon. 3/29/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/r/regularpolygon.html.Image Credits
- All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Revision History
3/29/2019: Clarified wording. Remove extraneous references to the manipulatives. (McAdams, David E.)12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
12/5/2018: Removed broken links, updated license, implemented new markup, implemented new Geogebra app. (McAdams, David E.)
8/7/2018: Changed vocabulary links to WORDLINK format. (McAdams, David E.)
12/31/2009: Added "References". (McAdams, David E.)
12/31/2008: Changed equations from HTML to images. (McAdams, David E.)
12/11/2008: Added 'Center of a Regular Polygon'. Changed circumcircle figure to manipulative. Added 'Incircles of Regular Polygons' (McAdams, David E.)
11/2/2008: Changed manipulative to GeoGebra. (McAdams, David E.)
6/11/2008: Added section on the central angle of a regular polygon and circumcircle. (McAdams, David E.)
4/18/2008: Initial version. (McAdams, David E.)
- Navigation
- Home
- Contents
-
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z - Teacher Aids
- Classroom Demos
- How To
- LIASP
- LIASP Home
- Conditions of Use
- Privacy Policy
- Donate to LIASP
- Help build this site
- About LIASP
- Contact LIASP
All Math Words Encyclopedia is a service of
Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License
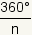 or
or
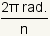 where n is the number of vertices of the polygon.
where n is the number of vertices of the polygon.