Topology
Pronunciation: /təˈpɒ.lə.dʒi/ ExplainTopology is the study of the properties of geometric figures that do not change under certain types of transformations called continuous maps. Two transformations that are continuous maps are dilation and reflection. Two transformations that are not continuous maps are cutting and gluing.
|
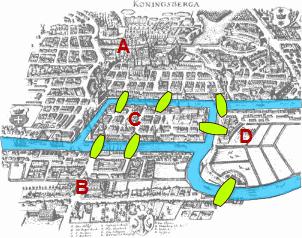
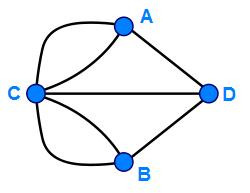
One of the first problems known to have been considered that falls within the discipline of topology is called "The Seven Bridges of Königsberg". Königsberg was a city in Prussia, which is now Kaliningrad, Russia. There were seven bridges in the city crossing a river and connecting two islands to each other and both sides of the river (see figure 1). The question had been posed, "Is it possible to cross each of the bridges once without crossing any of them a second time?" The answer was given by Leonhard Euler in 1736. In short, it is not possible to cross all seven bridges exactly once. Euler started by showing that the problem could be transformed into a set of three nodes connected by seven lines (see figure 2). The nodes represented each side of the river and the island. The lines each represented one of the bridges. The only way to travel from one node to another is via a line (a bridge). To travel all the bridges from any node to another node without crossing one twice, either the node must be a start or end point and have an odd number of lines, or the node must not be a start or end point and have an even number of lines. But, since only two nodes can be the start and end points, and all the nodes have an odd number of lines, it is impossible to transverse all the lines (cross all the bridges) exactly once. |
|
References
- McAdams, David E.. All Math Words Dictionary, topology. 2nd Classroom edition 20150108-4799968. pg 179. Life is a Story Problem LLC. January 8, 2015. Buy the book
Cite this article as:
McAdams, David E. Topology. 4/3/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/t/topology.html.Image Credits
- All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
- Seven Bridges of Königsberg: Maksim, commons.wikimedia.org. This file is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license. https://commons.wikimedia.org/wiki/File:Keningsbergo_pontoj_markitaj.png.
Revision History
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)12/4/2018: Removed broken links, updated license, implemented new markup. (McAdams, David E.)
5/5/2011: Initial version. (McAdams, David E.)
- Navigation
- Home
- Contents
-
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z - Teacher Aids
- Classroom Demos
- How To
- LIASP
- LIASP Home
- Conditions of Use
- Privacy Policy
- Donate to LIASP
- Help build this site
- About LIASP
- Contact LIASP
All Math Words Encyclopedia is a service of
Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License