Geometric Figure

Pronunciation: /ˌdʒi.əˈmɛt.rɪk ˈfɪg.jər/ Explain

A geometric figure is a set of one or more points in n-space. The most basic geometric figure is a point. All other geometric figures are made from points. Lines and curves are continuous one-dimensional sets of points.

All geometric figures exist in a space. A space has certain properties. Geometric figures in a space must be consistent with the properties of that space.

Geometric Figures in n-Space

The only geometric figure that can exist in a space with 0 or more dimensions is a point. A geometric figure that can exist only in a space with one or more dimensions is a linear figure. Examples of linear objects are lines, rays, and line segments. A geometric figure that can exist only in a space with 2 or more dimensions is a planar figure. Examples of planar figures are circles, squares, and parabolas. A geometric figure that can exist only in a space with 3 or more dimensions is a solid. Examples of solids are cubes, spheres, and paraboloids.

Any geometric figure that can exist in a 1 dimensional space can also exist in a 2 or more dimensional space. More generally, a geometric figure that can exist in an n-space can exist in a space with more than n dimensions.

Properties of Geometric Figures

Name	Illustration	Description
Boundary point		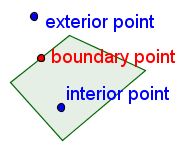A point is a boundary point of a figure if every neighborhood of the point contains points in the figure and points not in the figure. To visualize this, imagine a point in the figure that is not a boundary point. If one draws a small enough circle around that point, all points inside the circle will be part of the figure. The point can not be a boundary point. Only a point on the boundary fits this definition. Note that a boundary point may or may not be a part of the figure.
Boundary		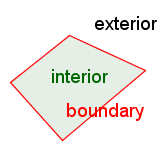The boundary of a geometric figure is the set of all the boundary points of the figure.
Interior		The interior of a geometric figure is all points that are part of the figure, but are not boundary points. Usually the interior of a geometric figure is what one thinks of when one thinks of an interior, but this is not necessarily so. Take, for example, a house. The interior of the house is considered to be the space inside the house. Now consider the outdoors (as opposed to the house and its interior). All parts of the outdoors are the interior of the outdoors and the interior of the house is the exterior of the outdoors.
Exterior		The exterior of a geometric figure is all points that are not part of the figure, and are not boundary points.
Open		A geometric figure is open if and only if some part of the boundary of the figure is not a part of the figure. An open boundary is conventionally drawn with a dotted or dashed line.
Closed		A geometric figure is closed if and only if all of the boundary of the figure is part of the figure. A closed boundary is conventionally drawn with solid line.
Bounded		A geometric figure is bounded if, in any direction, there is always a last point that is part of the figure. To visualize this, imagine a ray drawn from a point on the figure. If all such rays encounter a last point that is part of the figure, the figure is bounded.
Unbounded		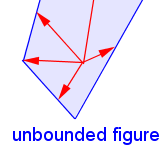A geometric figure is unbounded if, in any direction, there is no last point that is part of the figure. To visualize this, imagine a ray drawn from a point on the figure. If some such ray never encounters a last point that is part of the figure, the figure is unbounded.
Connected		A geometric figure is connected if, between all pairs of points that are part of the figure, there exists a path between the points that does not leave the figure.
Disconnected		A geometric figure is disconnected if, between any pair of points that are part of the figure, there exist no path between the points that does not leave the figure.
Dimension	None	The dimension of a geometric figure is hard to pin down without a discussion beyond the scope of this encyclopedia (definitely a college-level discussion). A brief example will have to do. A curve is a one-dimensional set of points. Yet a curve will not fit into a one dimensional space. A curve requires a space of at least 2 dimensions. A curve will fit into a 2 dimensional plane is called a planar curve. Consider also the surface of a sphere. The surface of a sphere has only 2 dimensions, yet it requires a 3-dimensional space to exist.
Table 1: Properties of Geometric Figures

Some Types of Geometric Figures

Illustration	Name	Description
Point		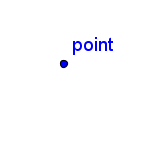An object of zero dimensions whose only property is location
Line		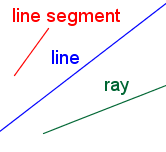An straight object of one dimension that goes on forever in both directions.
Line segment		A portion of a line with two endpoints.
Ray		A portion of a line with one endpoint.
Curve		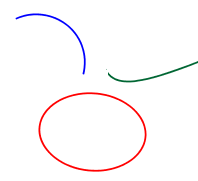A curved line. A curve may have 0, 1 or 2 endpoints.
Square		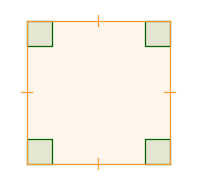A four-sided figure with straight sides that meet at right angles.
Circle		All points in a plane at the same distance from a center point.
Parabola		The shape made when graphing a quadratic equation.
Parallelepiped		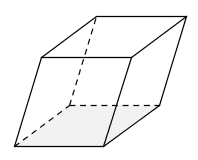A solid whose sides are parallelograms.
Sphere		All points in 3 dimensions that are the same distance from a center.
Hypersphere	None	All points in 4 dimensions that are the same distance from a center.
Table 3: Some Types of Geometric Figures.

References

1. McAdams, David E.. All Math Words Dictionary, geometric figure. 2nd Classroom edition 20150108-4799968. pg 85. Life is a Story Problem LLC. January 8, 2015. Buy the book

Cite this article as:

McAdams, David E. Geometric Figure. 12/21/2018. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/g/geometricfigure.html.

Image Credits

• All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Revision History

12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
7/10/2018: Removed broken links, updated license, implemented new markup, implemented new Geogebra protocol. (McAdams, David E.)
1/1/2010: Added "More Information" and "References". (McAdams, David E.)
4/18/2009: Initial version. (McAdams, David E.)