Factorial
Un factorial de n es el producto de todos los números enteros a partir de la 1 a n, inclusivo. La marca de exclamación (!) es el operador unario que representa factorial. La expresión “5!â€? se lee, “cinco factorialesâ€? y los medios 1·2·3·4·5 que iguales 120. Factorial cero (0!) se trata como un caso especial y se define para ser 0! = 1. A este nivel de las matemáticas, la n en n! debe ser un número entero no negativo.
En las matemáticas avanzadas, factoriales se define usando la
función Gamma:
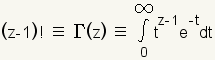 |
| Ecuación 1 |
Primeros 11 Factorials
| n | Fórmula | ¡n! |
|---|---|---|
| 0 | Ninguno | 1 |
| 1 | 1! = 1 | 1 |
| 2 | 2! = 1·2 | 2 |
| 3 | 3! = 1·2·3 | 6 |
| 4 | 4! = 1·2·3·4 | 24 |
| 5 | 5! = 1·2·3·4·5 | 120 |
| 6 | 6! = 1·2·3·4·5·6 | 720 |
| 7 | 7! = 1·2·3·4·5·6·7 | 5040 |
| 8 | 8! = 1·2·3·4·5·6·7·8 | 40.320 |
| 9 | 9! = 1·2·3·4·5·6·7·8·9 | 362.880 |
| 10 | 10! = 1·2·3·4·5·6·7·8·9·10 | 3.628.800 |
| Cuadro 1 | ||
Trabajo con Factorials
Puesto que los factorials consiguen muy grandes muy rápidamente (véase el cuadro 1), ellos puede ser difÃcil de calcular sin una calculadora. Sin embargo, cuando están utilizadas en matemáticas, las ecuaciones usando factorials implican generalmente razóns de factorials. Puesto que los factorials por definición tienen muchos factores comunes, estos problemas se pueden reducir en dificultad cancelando factores comunes.
Para entender esto, comience con la definición de una
combinación:
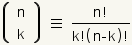 |
| Ecuación 1 |
Si uno desea calcular
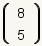 , la fórmula es: , la fórmula es:
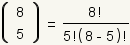 . .
|
Primero, ponga los factorials en escrito:
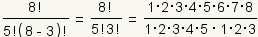 . .
|
Ahora utilice la propiedad de multiplicarse por 1
para cancelar todos los:
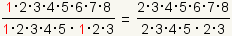 . .
|
Ahora cancele los factores que son iguales:
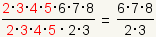 . .
|
Ahora busque los factores restantes que tienen factores comunes. En el caso, 2·3 = 6 los 6 en la tapa cancela tan los 2·3 en la parte inferior:
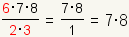 . .
|
Esto ahora se ha convertido en un problema simple de la multiplicación. Puesto que
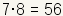 , hay exactamente 56 maneras que cinco objetos seleccionados de una piscina de ocho objetos pueden ser arreglados. Asà pues , hay exactamente 56 maneras que cinco objetos seleccionados de una piscina de ocho objetos pueden ser arreglados. Asà pues
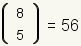 . .
|
Más información
- factorial. buscon.rae.es. Real Academia Española. 2009-04-03. http://buscon.rae.es/draeI/SrvltConsulta?TIPO_BUS=3&LEMA=factorial.
Citar este artÃculo como:
Factorial. 2009-04-03. Enciclopedia de Todas las Palabras de la Matemáticas. Life is a Story Problem.org. https://www.allmathwords.org/es/f/factorial.html.
Traducciones
créditos de imagen
- Todas las imágenes y manipulatives están por David McAdams a menos que estén indicadas de otra manera. Todas las imágenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.
La historia de revisión
2009-04-03: Traducido automáticamente por BabelFish. (babelfish.yahoo.com.)
2008-12-29: Ecuaciones corregidas (McAdams, David.)
2008-04-23: Versión inicial (McAdams, David.)
- Navegación
- Home
- Contenido
-
# A B C D E F G H I J L M N O P Q R S T U V X Y - Ayudas del profesor
- Demostraciones de la Clase
- Referencia recÃproca
- GeometrÃa de NYSDE
- LIASP
- LIASP Home
- Condiciones del uso
- PolÃtica de aislamiento
- Done a LIASP
- Estructura de la ayuda este sitio
- Sobre LIASP
- LIASP del Contacto
Enciclopedia de Todas las Palabras de la Matemáticas es un servicio de
Life is a Story Problem.org.
Los derechos reservados ©2005-2009 de Life is a Story Problem.org. Todos los derechos reservados.
 Este trabajo
se autoriza debajo de una
Creative Commons Attribution-Noncommercial-Share Alike 3.0 License
Este trabajo
se autoriza debajo de una
Creative Commons Attribution-Noncommercial-Share Alike 3.0 License