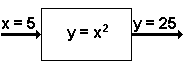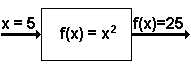Función: Un conjunto de los pares ordenados donde las variables independientes, o la entrada, generan exactamente un valor de la salida (variable dependiente).

Función

La “función etiquetada caja� con una flecha que entraba la caja etiquetó la “entrada� y una flecha que salía de la caja etiquetó “salida�.
Cuadro 1: Función

Una función se puede considerar como una caja con una entrada y una salida. Para cada entrada que entre la caja, un de salida única sale de la caja. Véase el cuadro 1. Para cualquier entrada particular que entre la caja, la misma salida sale siempre de la caja.

“X^2 etiquetado caja� con una flecha que entraba la caja etiquetó “5� y una flecha que salía de la caja etiquetó “25�.
Cuadro 2: Función f(x)=x2

En el cuadro 2, se etiqueta la función y = x2. “y = x2� es la regla para transformar la entrada en la salida. Para cualquier número entre en la función, ajustan el número para conseguir la salida. Observe que cada vez que el número 5 se entra en la función, el número 25 es la salida. La entrada de 5 generará solamente la salida de 25.

“G etiquetado caja (x)= {(a, b), (b, c), (c, d), (d, e), (e, a)}� con una flecha que entraba la caja etiquetó “x� y una flecha que salía de la caja etiquetó “g (x)�.
Cuadro 3: Función g (x)= {(a, b), (b, c), (c, d), (d, e), (e, a)}

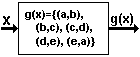
Las funciones se definen matemáticamente como conjunto de pares ordenados. El primer valor en los pares ordenados es la entrada, y el segundo valor es la salida. Los pares ordenados para la función en el cuadro 3 serían (5.25). 5 es la entrada y 25 es la salida. Para una función, el primer valor no puede ser repetido. Note que esto permite exactamente uno hecho salir para cada entrada.

La definición de una función como un conjunto de pares ordenados permite que definamos las funciones que no utilizan números. Tome el conjunto {a, b, c, d, e}. Si la función g(x) se define como g(x) = {(a, b), (b, c), (c, d), (d, e), (e, a)}, uno puede decir qué sale de la función dada qué entra. Si a es la entrada, b es la salida.

Para muchas funciones, usando un conjunto enumerado de pares ordenados definir la función no es práctica, puesto que hay infinitamente muchas entradas y salidas. Una regla se utiliza típicamente en estos casos. Una regla puede definir infinitamente muchos pares ordenados sin tener que enumerar cada par ordenado.

La “función etiquetada caja� con una flecha que entraba la caja etiquetó “variable independiente� y una flecha que salía de la caja etiquetó “variable dependiente�.
Cuadro 4: Función

“F etiquetada caja (x)=x^2� con una flecha que entra la caja etiquetada “variable independiente� y una flecha que sale de la caja etiquetada “variable dependiente�.
Cuadro 5: Función

En la álgebra de números reales, las funciones se definen usando variables. La entrada se llama la variable independiente. La salida se llama la variable dependiente. Un valor particular de la variable independiente, o de la entrada, genera exactamente un valor de la variable dependiente.

Un ejemplo de una función algebraica es y = x2. x es variable independiente. x puede ser cualquier número que pueda ser ajustado. x es tan independiente todo lo demás. y es la variable dependiente. El valor de y depende del valor del x. Por ejemplo: Si x = 5, y = 25. Cuando x es 5, y no puede ser todo menos 25. Esto es porque la función indica y = x2, así que y debe siempre ser el cuadrado del x.

Notación de la función

La función f(x)=3x+2 que f (x) es la variable dependiente, x es la variable independiente y 3x+2 es la regla de la transformación.
Cuadro 6: Notación de la función

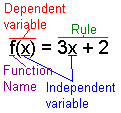
La notación de la función es manera de uso general de anotar funciona. En el ejemplo en el cuadro 6, x es la variable independiente, f es el nombre de función, f(x) es la variable dependiente, y 3x+2 es la regla para transformar x a f(x). Vea también la notación de la función.

Dominio y rango de funciones

Cada función tiene un dominio y una rango. El dominio es todos los valores que la variable independiente puede tomar. Vea el dominio para más información. La rango es todos los valores que la variable dependiente puede tomar. Vea la rango para más información.

Representaciones de funciones

Las funciones se pueden representar en gran medida. El cuadro 7 demuestra las maneras mas comunes.
RepresentaciónDescripción
{(1.3), (2.7), (4, - 5)}Un conjunto de pares ordenados donde está la entrada y el segundo valor el primer valor es la salida.
f (n) donde está un número entero y una f n positivos (n) está el n.de número de Fibonacci.Una descripción escrita.
y = 3x + 2Una ecuación con una variable independiente y una variable dependiente
f (x) = x2Notación de la función
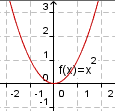Un gráfico de y=x^2Un gráfico donde el eje horizontal representa la variable independiente y el eje vertical representa la variable dependiente.
xf (x)
14
27
3-2
46
Una tabla donde una columna o fila representa la variable independiente. Otra columna o fila representa la variable dependiente.
Cuadro 7: Representaciones de funciones

Operaciones en funciones

Las funciones que se definen sobre números reales se pueden agregar, restar, multiplicar y dividir apenas como números. También, las funciones pueden ser compuestas.

OperaciónDefiniciónAssociativityCommutativity
Adición(f+g) (x) = f (x) + g (x)(f+ (g+h)) (x) = ((f+g)+h) (x)(f+g) (x) = (g+f) (x)
Substracción(f-g) (x) = f (x) - g (x)(f (g-h))(x) = ((f-g) - h) (x)(f-g) (x) ≠ (g-f) (x)
Multiplicación(f·g) (x) = f (x) · g (x)(f·(g·h)) (x) = ((f·g)·h) (x)(f·g) (x) = (g·f) (x)
División(f÷g) (x) = f (x) ÷ g (x)(f÷ (g÷h)) (x) = ((f÷g)÷h) (x)(f÷g) (x) ≠ (g÷f) (x)
Composición(f°g) (x) = f (g (x))(f° (g°h)) (x) = ((f°g)°h) (x)(f°g) (x) ≠ (g°f) (x)
Cuadro 8: Resumen de operaciones en funciones.

Adición y resta de funciones

La suma de funciones se define como (f + g) (x) = f (x) + g (x). Para agregar dos funciones, agregue todos términos semejantes de cada función. La suma de funciones es asociativa: (f+ (g+h)) (x) = ((f+g)+h) (x). La suma de funciones es comutativa: (f+g) (x) = (g+f) (x).

PasoEcuacionesDescripción
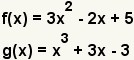1f (x)=3x^2-2x+5, g (x)=x^3+3x-3Éstas son las funciones a agregar.
2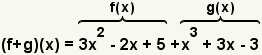(f+g) (x)= (3x^2-2x+5)+ (x^3+3x-3) donde 3x^2-2x+5=f (x) y x^3+3x-3=g (x)Utilice la definición de la suma de la función para crear la nueva función.
3(f+g) (x)=x^3+3x^2-2x+3x+5-3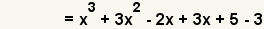Utilice la propiedad comutativa de la suma para poner los términos de la nueva función en la orden del grado.
4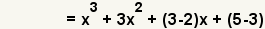(f+g) (x)=x^3+3x^2+ (- 2+3) x+5-3Utilice la propiedad distributiva de la multiplicación sobre la suma y la resta para comenzar a combinar términos semejantes.
5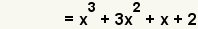(f+g) (x)=x^3+3x^2+x+2Simplifique la suma.
Cuadro 9: Adición de funciones

Para restar dos funciones, reste todos términos semejantes de cada función. La definición de la resta de la función es (f-g) (x) = f (x) - g (x). La resta de funciones es asociativa: (f (g-h))(x) = ((f-g) - h) (x). La resta de funciones no es comutativa: (f-g)(x) ≠ (g-f)(x).

PasoEcuacionesDescripción
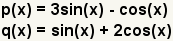1p (x)=3sin (x) - lechuga romana (x), q (x)=sin (x)+2cos (x)Éstas son las funciones a restar.
2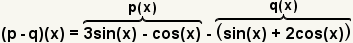(p-q) (x)=3sin (x) - lechuga romana (x) - (pecado (x)+2cos (x))Utilice la definición de la resta de la función para formar la nueva función.
3(p-q) (x)=3sin (x) - lechuga romana (x) - pecado (x) - 2cos (x)Distribuya la negada sobre la segunda función.
4(p-q) (x)=3sin (x) - pecado (x) - lechuga romana (x) - 2cos (x)Utilice la propiedad comutativa de la suma para poner los términos de la nueva función en la orden del grado.
5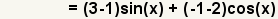(p-q) (x)= (3-1) pecado (x)+ (- 1-2) lechuga romana (x)Utilice la propiedad distributiva de la multiplicación sobre la suma y la resta para comenzar a combinar términos semejantes.
6(p-q) (x)=2sin (x) - 3cos (x)Simplifique la suma.
Cuadro 10: Substracción de funciones

Multiplicación de funciones

Para multiplicar dos funciones, multiplique cada término de la primera función por cada término de la segunda función. Se define la multiplicación de la función como (f·g)(x) = f(x) · g(x). La multiplicación de funciones es asociativa: f(x)·(g(x)·h(x)) = (f(x)·g(x))·h(x). La multiplicación de funciones es comutativa: f(x)·g(x) = g(x)·f(x).

PasoEcuacionesDescripción
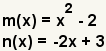1m (x)=x^2-2, n (x)=-2x+3Éstas son las funciones a multiplicarse.
2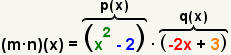(m*n) (x)= (x^2-2) * (- 2x+3)Utilice la definición de la multiplicación de la función para formar la nueva función.
3(m*n) (x)=x^2* (- 2x) +x^2*3+ (- 2) * (- 2x) + (- 2) (3)Multiplique cada término a partir de los primeros tiempos de la función cada término de la segunda función. Puesto que ambas funciones son binomios, utilice el método de la HOJA.
4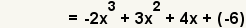(m*n) (x)=-2x^3+3x^2+4x+ (- 6)Simplifique la multiplicación.
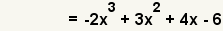5(m*n) (x)= (f*g) (x)=-2x^3+3x^2+4x-6Simplifique paréntesis.
Cuadro 11: Multiplicación de funciones

División de funciones

A las funciones de divisoria, cree una fracción con el dividendo en el numerador y el divisor en el denominador. Simplifique la fracción, si es posible. La definición de la división de la funci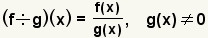ón es:
¡(f/g) (x)=f (x)/g (x), g (x)!=0.
La división de funciones es asociativa: f (x) (g (x)/h (x)) = (f (x)/g (x)) /h (x). La división de funciones no es comutativa: f(x)/g(x) ≠ g(x)/f(x).

PasoEcuacionesDescripción
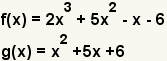1f (x)=2x^2+5x^2-x-6, g (x)=x^2+5x+6Éstas son las funciones a dividir.
2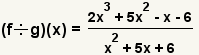(f/g) (x)= (2x^2+5x^2-x-6)/(x^2+5x+6)Utilice la definición de la división de la función para formar la nueva función.
3(f/g) (x)= ((x-1) (x+2) (2x-3))/((x+2) (x+3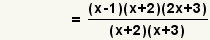))Encuentre los factores comunes para el numerador y el denominador.
4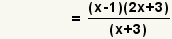(f/g) (x)= ((x-1) (2x-3))/((x+3))Elimine los factores comunes.
5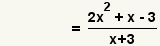(f/g) (x)= (2x^2+x-3)/(x+3)Reescriba la función usando polinomios en forma estándar.
Cuadro 12: División de funciones

Composición de funciones

La composición de funciones está tomando la función de una función. Por ejemplo, si f(x) = x2 + 1, y g(x) = x - 2, entonces la composición de f(x) y g(x), escrita el f°g(x) es f(g(x)) = (x-2)2 + 1 = (x2 - 4x + 2) + 1 = x2-4x + 3 la composición funciones es asociativo: f°(g°h)(x) = (f°g)°h(x). La composición de funciones no es comutativa: f°g(x) ≠ g°f(x).

PasoEcuacionesDescripción
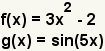1f (x)=3x^2-2, g (x)=sin (5x)Éstas son las funciones a componer.
2(f°g) (x)=3 (pecado (5x))^2-2Utilice la definición de la composición para componer las dos funciones.
3(f°g) (x)=3sin^2 (5x) - 2Simplifique la expresión.
2(g°f) (x)=sin (5 (3x^2-2))Ahora encuentre g°f. Utilice la definición de la composición para componer las dos funciones.
3(g°f) (x)=sin (15x^2-10)Simplifique usando la propiedad distributiva de la multiplicación sobre la suma y la resta.
Cuadro 13: Composición de funciones

Más información

  • McAdams, David. Dominio. AllMathWords.org. Life is a Story Problem.org. 2009-04-03. https://www.allmathwords.org/article.aspx?lang=es&id=Domain.
  • McAdams, David. Gama. AllMathWords.org. Life is a Story Problem.org. 2009-04-03. https://www.allmathwords.org/article.aspx?lang=es&id=Range.
  • McAdams, David. Notación de la función. AllMathWords.org. Life is a Story Problem.org. 2009-04-03. https://www.allmathwords.org/article.aspx?lang=es&id=Function%20Notation.
  • McAdams, David. Recta vertical prueba. AllMathWords.org. Life is a Story Problem.org. 2009-04-03. https://www.allmathwords.org/article.aspx?lang=es&id=Vertical%20Line%20Test.
  • función. buscon.rae.es. Real Academia Española. 2009-04-03. http://buscon.rae.es/draeI/SrvltConsulta?TIPO_BUS=3&LEMA=función.

Citar este artículo como:
Función. 2009-04-03. Enciclopedia de Todas las Palabras de la Matemáticas. Life is a Story Problem.org. https://www.allmathwords.org/es/f/function.html.

Traducciones

créditos de imagen

  • Todas las imágenes y manipulatives están por David McAdams a menos que estén indicadas de otra manera. Todas las imágenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.

La historia de revisión


2009-04-03: Traducido automáticamente por BabelFish. (babelfish.yahoo.com.)
2009-03-10: Definición aclarada de la notación de la función (McAdams, David.)
2009-02-11: Sección agregada en operaciones en funciones (McAdams, David.)
2008-08-02: Reescribió el artículo entero (McAdams, David.)
2007-08-20: Agregue esta historia de revisión (McAdams, David.)
2007-07-12: Versión inicial (McAdams, David.)

Enciclopedia de Todas las Palabras de la Matemáticas es un servicio de Life is a Story Problem.org.
Los derechos reservados ©2005-2009 de Life is a Story Problem.org. Todos los derechos reservados.
Creative Commons License Este trabajo se autoriza debajo de una Creative Commons Attribution-Noncommercial-Share Alike 3.0 License