Box and Whisker Plot

Pronunciation: /bɒks ənd ˈʰwɪs.kər plɒt/ Explain

A box and whisker plot is used to show the distribution of a data set.[2] Each quartile is marked on the graph, and a box is drawn to represent the 2nd and 3rd quartiles. Lines are drawn to represent the 1st and 4th quartiles. These are the 'whiskers'. The box and whisker plot in figure 1 represents the data set { 2, 2, 3, 4, 5, 5, 6, 7, 8, 9 }.

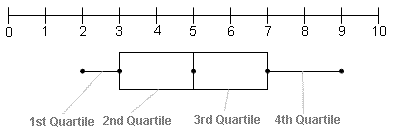Box and whisker plot
Figure 1: Box and Whisker Plot

A box and whisker plot is also called a box plot or a boxplot.

How to Draw a Box and Whisker Plot

For this example, use the data set { 1, 8, 4, 3, 9, 3, 6, 4, 7 }.

StepDescriptionExample
1 Draw a number line that will contain the box and whisker plot. 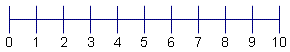Number line from 0 to 10.
2 Determine the median of the data set. The median of this data set is 4. Draw a vertical line under the 4. 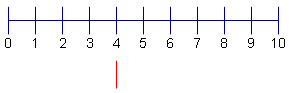Number line from 0 to 10 with a line marking 4.
3 Now calculate the start of the 1st quartile. Take the first half of the data set: { 1, 3, 3, 4 }. Find the median of the first half of the data set. In this case, the median is 3 + 3 = 6. 6 / 2 = 3. Make a line under the 3. 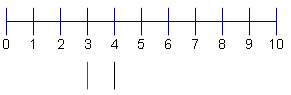Number line from 0 to 10 with a line under the numbers 3-4.
4 Complete the box for the 2nd quartile. 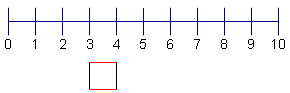Number line from 0 to 10 with a box from under 3-4 showing the 2nd quartile.
5 Calculate the start of the 4th quartile. Take the second half of the data set: { 6, 7, 8, 9 }. Find the median of the second half of the data set. In this case, the median is 7 + 8 = 15. 15 / 2 = 7.5. Make a line under 7.5. 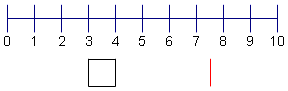Number line from 0 to 10 with a line under the numbers 3-4.
6 Complete the box for the 3rd quartile. 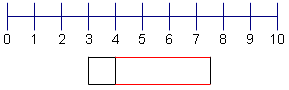Number line from 0 to 10 with a box from under 3-4 showing the 2nd quartile and a box under 4-7.5 showing the 3rd quartile.
7 Now draw a point to show the start of the 1st quartile. Do not include any outliers. 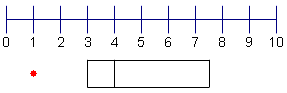Number line from 0 to 10 with a box from under 3-4 showing the 2nd quartile and a box under 4-7.5 showing the 3rd quartile, and a point under 1 marking the start of the 1st quartile.
8 Connect the point to the middle of the 2nd quartile line. 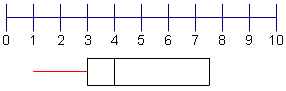Number line from 0 to 10 with a box from under 3-4 showing the 2nd quartile and a box under 4-7.5 showing the 3rd quartile, and a line from 1-3 showing the first quartile.
9 Now draw a point to show the end of the 4th quartile. Do not include any outliers. 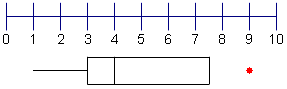Number line from 0 to 10 with a box from under 3-4 showing the 2nd quartile and a box under 4-7.5 showing the 3rd quartile, and a line from 1-3 showing the first quartile, and a point under 9 showing the end of the 4th quartile.
10 Connect the point to the middle of the 3rd quartile line. Your box and whisker plot is now complete. 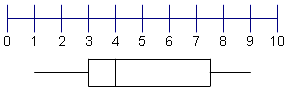Number line from 0 to 10 with a box from under 3-4 showing the 2nd quartile and a box under 4-7.5 showing the 3rd quartile, and a line from 1-3 showing the first quartile, and a line from 7.5-9 showing the 4th quartile.

References

  1. McAdams, David E.. All Math Words Dictionary, box and whisker plot. 2nd Classroom edition 20150108-4799968. pg 28. Life is a Story Problem LLC. January 8, 2015. Buy the book

More Information

  • Box and Whisker Plots. mathbits.com. Mathbits.com. 6/22/2018. http://mathbits.com/MathBits/TISection/Statistics1/BoxWhisker.htm.

Cite this article as:

 McAdams, David E. Box and Whisker Plot. 4/12/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/b/boxandwhiskerplot.html.

Image Credits

Revision History

4/12/2019: Changed equations and expressions to new format. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
6/22/2018: Removed broken links, updated license, implemented new markup. (McAdams, David E.)
11/25/2009: Added "References" to 'Box Plot' and 'Boxplot'. (McAdams, David E.)
6/7/2008: Corrected spelling. (McAdams, David E.)
3/18/2008: Initial version. (McAdams, David E.)

All Math Words Encyclopedia is a service of Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License