Ceiling Function

Pronunciation: /ˈsil.ɪŋ ˈfʌŋk.ʃən/ Explain

Figure 1: Graph of the ceiling function

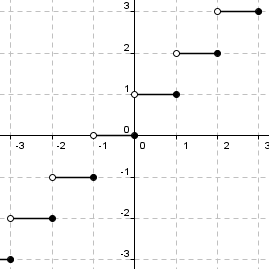
The ceiling function returns the smallest integer greater than or equal to the argument. The ceiling function of x is denoted ⌈x⌉. In some computer languages the ceiling function is represented by 'ceil(x)'. The ceiling function is a type of step function. Examples x ⌈x⌉ -4 ⌈-4⌉ = -4 -3.5 ⌈-3.5⌉ = -3 -0.5 ⌈-0.5⌉ = 0 0 ⌈0⌉ = 0 0.5 ⌈0.5⌉ = 1 1.375 ⌈1.375⌉ = 2 22.2 ⌈22.2⌉ = 23 1394.75 ⌈1394.75⌉ = 1395 Table 1

References

1. McAdams, David E.. All Math Words Dictionary, ceiling function. 2nd Classroom edition 20150108-4799968. pg 30. Life is a Story Problem LLC. January 8, 2015. Buy the book
2. Bettinger, Alvin K. and Englund, John A.. Algebra and Trigonometry. pg 57. www.archive.org. Last Accessed 6/25/2018. http://www.archive.org/stream/algebraandtrigon033520mbp#page/n74/mode/1up/search/greatest. Buy the book

More Information

• McAdams, David E.. Floor Function. allmathwords.org. All Math Words Encyclopedia. Life is a Story Problem LLC. 6/27/2018. https://www.allmathwords.org/en/f/floorfunction.html.

Cite this article as:

McAdams, David E. Ceiling Function. 4/13/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/c/ceilingfunction.html.

Image Credits

• All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Revision History

3/1/2019: Corrected formatting. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
6/25/2018: Removed broken links, updated license, implemented new markup, updated GeoGebra apps. (McAdams, David E.)
11/19/2009: Added text about step function and ceil(). (McAdams, David E.)
10/25/2009: Initial version. (McAdams, David E.)