Circumcenter

Pronunciation: /ˈsɜr.kəmˌsɛn.tər/ Explain

Click on the blue points and drag them to change the figure Manipulative 1 - Circumcircle of a Triangle Created with GeoGebra.

The circumcenter of a polygon is the center of the circle that intersects all vertices of the polygon exactly once. The circumcircle of a polygon is the circle that intersects all vertices of the polygon. The circumcenter of a triangle is found at the intersection of the perpendicular bisectors of the sides. A circumradius of a polygon is a radius of the circumcircle.

How to Construct the Circumcenter and Circumcircle of a Triangle

1		Pick any one side of a triangle and construct its perpendicular bisector.
2		Pick one of the remaining sides of a triangle and construct its perpendicular bisector.
3		Draw a circle with the center at the intersection of the two bisectors and a radius of the distance between the intersection and any vertex of the triangle.

How to Construct the Circumcenter and Circumcircle of a Regular Polygon

Step	Illustration	Discussion and Justification
1		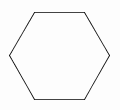The center of a regular polygon is at the point of concurrency of perpendicular bisectors of any two sides that are not opposite each other.
2		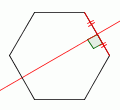Draw the perpendicular bisector of any side.
3		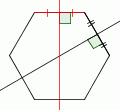Draw the perpendicular bisector of any other side that is not opposite the side you used in step 2.
4		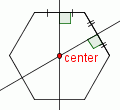Label the intersection of the two perpendicular bisectors as 'center'.
5		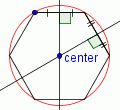Draw a circle with a center at the point labeled 'center' and the edge at any vertex. This is the circumcircle.
Table 2 - How to construct the center and circumcircle of a regular polygon

References

1. McAdams, David E.. All Math Words Dictionary, circumcenter. 2nd Classroom edition 20150108-4799968. pg 33. Life is a Story Problem LLC. January 8, 2015. Buy the book

More Information

• McAdams, David E.. Center. allmathwords.org. Life is a Story Problem LLC. 6/27/2018. https://www.allmathwords.org/en/c/center.html.

Cite this article as:

McAdams, David E. Circumcenter. 3/5/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/c/circumcenter.html.

Image Credits

• All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Revision History

3/5/2019: Added word links. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
12/16/2018: Changed incenter to circumcenter. (McAdams, David E.)
6/25/2018: Removed broken links, updated license, implemented new markup, updated GeoGebra apps. (McAdams, David E.)
4/28/2011: Added circumradius. (McAdams, David E.)
10/13/2010: Generalize article to deal with all polygons, rather than just triangles. Added section on constructing the circumcenter and circumcircle of a regular polygon. (McAdams, David E.)
1/9/2010: Added "References". (McAdams, David E.)
11/15/2008: Changed manipulative to Geogebra. (McAdams, David E.)
7/7/2008: Corrected link errors. Corrected spelling (McAdams, David E.)
3/25/2008: Revised More Information to match current standard. (McAdams, David E.)
8/24/2007: Simplified figure 1. Added reference to triangle. Added circumcircle (McAdams, David E.)
7/30/2007: Initial version. (McAdams, David E.)