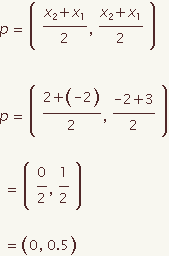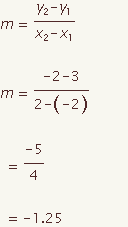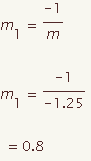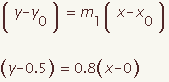Perpendicular Bisector

Pronunciation: /ˌpɜr.pənˈdɪk.jə.lər ˈbaɪ.sɛk.tər/ Explain
Click on the blue points and drag them to change the figure.

Note that the perpendicular bisector is at right angles to the line segment.
Manipulative 1 - Perpendicular Bisector of a Line Segment Created with GeoGebra.

A perpendicular bisector is a line that bisects a line segment and is perpendicular to the line segment. In manipulative 1, line segment AB is the line segment being bisected. The red line is the perpendicular bisector. Point C is the midpoint of line segment AB.

Properties of a Perpendicular Bisector

Click on the blue points and drag them to change the figure.

Is the any position of C where the two red line segments are not the same length?
Manipulative 2 - Perpendicular Bisector Property Created with GeoGebra.

Each point on a perpendicular bisector are the same distance from the endpoints. Since all points on a circle are the same distance from the center of the circle, two circles of the same size can be used to find a perpendicular bisector.

In manipulative 2, point D is the same distance from the center of each of the circles, meaning AD ≡ BD. As the radius AD changes, the points D and E are always on the perpendicular bisector. Click on point D and drag it to trace the perpendicular bisector.

The perpendicular bisectors of the sides of a triangle meet at the circumcenter of the triangle.

Click on the blue points and drag them to change the figure

Manipulative 3 - Circumcircle of a Triangle Created with GeoGebra.

The perpendicular bisectors of the sides of a triangle intersect at a point called the circumcenter of the triangle.

How to Construct a Perpendicular Bisector

Table 1 shows the steps to create a perpendicular bisector using a straight edge and a compass. Click on the blue points in each of the manipulatives and drag them to change the figure.

StepManipulativeDescriptionJustification
blank space
Line segment AB is the line segment to bisect. These are the criteria.
1
Draw a circle with center A and radius AB. Euclid Elements Book 1 Postulate 3: A circle can be draw with any center and any radius.
2
Draw a circle with center B and radius BA. Euclid Elements Book 1 Postulate 3: A circle can be draw with any center and any radius.
3
Mark the intersections of the circles as points C and D. An intersection is a point of concurrency.
4
Draw a line through points C and D. This line is the perpendicular bisector. Euclid. Elements Book 1 Postulate 1. A line can be drawn from any point to any point.
5
The intersection of line segment AB and line segment CD is the midpoint of line segment AB. An intersection is a point of concurrency.
Table 1: Constructing a perpendicular bisector.

How to Find the Equation of a Perpendicular Bisector

Click on the blue points and drag them to change the figure.

Why is there different equations if the perpendicular bisector is vertical or horizontal?
Manipulative 10 - Equation of a Perpendicular Bisector of a Line Created with GeoGebra.

The equation of a perpendicular bisector can be calculated for a given line segment with end points (x1, y1) and (x2, y2). This demonstration will show how to calculate the equation of a perpendicular bisector in point slope form.

StepEquationDescription
1 p=((x2+x1)/2,(y2+y1)/2) gives p=0.5 First calculate the location of midpoint.
2 m=((y2-y1)/(x2-x1)) gives m=-1.25 Calculate the slope of the line segment AB.
3 m1=-1/m gives m1=0.8 Calculate the slope of the perpendicular line using the slope of line segment AB.
4 y-y0=m1(x-x0) gives y-0.5=0.8(x-0) Put the slope of the perpendicular line and the coordinates of the midpoint into and equation in point slope form.
Table 2: Calculating the equation of a perpendicular bisector

References

  1. McAdams, David E.. All Math Words Dictionary, perpendicular bisector. 2nd Classroom edition 20150108-4799968. pg 137. Life is a Story Problem LLC. January 8, 2015. Buy the book

More Information

  • Dendane, A. Perpendicular Bisector. Analyze Math. 3/12/2009. http://www.analyzemath.com/Geometry/PerpendicularBisector/PerpendicularBisector.html.
  • Euclid of Alexandria. Elements. Clark University. 9/6/2018. https://mathcs.clarku.edu/~djoyce/elements/elements.html.

Cite this article as:

 McAdams, David E. Perpendicular Bisector. 4/29/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/p/perpendicularbisector.html.

Image Credits

Revision History

4/29/2019: Changed equations and expressions to new format. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
12/1/2018: Removed broken links, updated license, implemented new markup, updated geogebra app. (McAdams, David E.)
8/7/2018: Changed vocabulary links to WORDLINK format. (McAdams, David E.)
11/15/2008: Initial version. (McAdams, David E.)

All Math Words Encyclopedia is a service of Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License