Complex Conjugate

Pronunciation: /kəmˈplɛks ˈkɒn.dʒə.gɪt/ Explain

Complex conjugates are two complex numbers of the form a + bi and a - bi where a and b are real numbers.^[3] Complex conjugates are denoted using a bar over the variable: If z = a + bi then z = a - bi Complex conjugates have the property that, when added together, the result is a real number.

Complex conjugates also have the property that, when multiplied together, the result is a real number.

Complex conjugates are usually used when dividing complex numbers.

Properties of Complex Conjugates

Equation	Description
(z + w) = z + w	The conjugate of a sum is equal to the sum of the conjugates.
(z - w) = z - w	The conjugate of a difference is equal to the difference of the conjugates.
(z · w) = z · w	The conjugate of a
(z / w) = z / w
|z| = |z|	The magnitude of a complex number is the same as the magnitude of its complement.
|z2| = z·z = z·z	The magnitude of the square of a complex number equals the complex number multiplied by its conjugate.
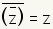	The conjugate of the conjugate of a complex number equals the original complex number.
ez = (ez)	Euler's number (e) raised to the conjugate of a complex number is equal to the conjugate of Euler's number raised to the complex number.
Table 1 - Properties of complex conjugates

References

1. McAdams, David E.. All Math Words Dictionary, complex conjugate. 2nd Classroom edition 20150108-4799968. pg 39. Life is a Story Problem LLC. January 8, 2015. Buy the book
2. conjugate complex number. merriam-webster.com. Encyclopedia Britannica. Merriam-Webster. Last Accessed 6/25/2018. https://www.merriam-webster.com/dictionary/conjugate%20complex%20number. Buy the book
3. Phillips, E. G.. Functions of a Complex Variable. 8th edition. pp 4-5,14. www.archive.org. Oliver and Boyd. 1961. Last Accessed 6/25/2018. http://www.archive.org/stream/functionsofacomp029605mbp#page/n17/mode/1up/search/conjugate. Buy the book

Cite this article as:

McAdams, David E. Complex Conjugate. 4/13/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/c/complexconjugates.html.

Image Credits

• All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Revision History

12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
6/25/2018: Removed broken links, updated license, implemented new markup, updated GeoGebra apps. (McAdams, David E.)
1/17/2010: Added "References". (McAdams, David E.)
11/25/2008: Changed equations to images. (McAdams, David E.)
7/8/2008: Changed equations from images to hot_Eqn. (McAdams, David E.)
3/25/2008: Revised More Information to match current standards. (McAdams, David E.)
2/13/2008: Added z-bar notation. (McAdams, David E.)
7/12/2007: Initial version. (McAdams, David E.)