Golden Section

Pronunciation: /ˈgoʊl.dən ˈsɛk.ʃən/ Explain

Click on the blue points and drag them to change the figures. What does not change when you change each figure? Manipulative 1 - Golden Section Created with GeoGebra.

The golden section is the ratio that divides a line segment into two parts such that the ratio of the length of the whole to the length of the larger segment is the same as the ratio of the length of the larger segment to the smaller segment: 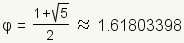. The golden section is also called the golden ratio, golden mean and divine proportion. The value of the golden section is represented by the Greek letter φ (phi). The value of the golden section is A golden rectangle is a rectangle where the ratio of the length of the sides is φ. A golden triangle is an isosceles triangle where the ratio of the length of the legs to the length of the base is φ. The golden triangle was used by Euclid to approximate the value of φ.

Derivation of the golden section

The value of the golden section is derived using the quadratic formula. Table 1 shows the derivation.

Step	Formula	Description
1		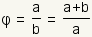Start with the definition of the golden section.
2		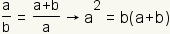Cross multiply.
3		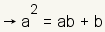Apply the distributive property of multiplication over addition and subtraction.
4		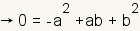Use the additive property of equality to add -a2 to both sides of the equation.
5		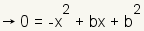Use the substitution property of equality to substitute x for a.
6		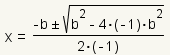Apply the quadratic formula.
7		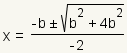Simplify the multiplication
8		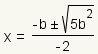Simplify the addition inside the parenthesis
9		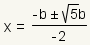Simplify the square root.
10		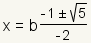Use the distributive property of multiplication over addition and subtraction to pull b out of the fraction.
11		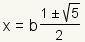Multiply the numerator and denominator of the fraction by -1.
12		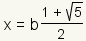Since a negative number does not make sense here, change the ± to +.
13		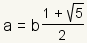Use the substitution property of equality to substitute a back in for x.
14		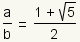Use the multiplication property of equality to multiply both sides of the equation by 1 / b.
15		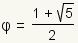Since definition of the golden section states φ = a / b, use the substitution property of equality to substitute φ for a / b.
Table 1 - Derivation of the golden section.

Representations of φ

Many different ways to represent φ have been found. One way to represent φ is the repeating fraction

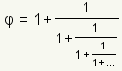
References

1. McAdams, David E.. All Math Words Dictionary, golden section. 2nd Classroom edition 20150108-4799968. pg 86. Life is a Story Problem LLC. January 8, 2015. Buy the book

More Information

• Euclid of Alexandria. Elements. Clark University. 9/6/2018. https://mathcs.clarku.edu/~djoyce/elements/elements.html.

Educator Resources

• Proportionality - Modeling the Future. NASA LaRC Office of Education. 2/18/2010. http://www.archive.org/details/NasaConnect-Proportionality-ModelingTheFuture/index.htm.

Cite this article as:

McAdams, David E. Golden Section. 4/21/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/g/goldensection.html.

Image Credits

• All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Revision History

4/21/2019: Updated equations and expressions to new format. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
7/10/2018: Removed broken links, updated license, implemented new markup, implemented new Geogebra protocol. (McAdams, David E.)
2/8/2010: Added "References". (McAdams, David E.)
11/26/2008: Changed equations to images. (McAdams, David E.)
11/18/2008: Changed manipulative to GeoGebra. (McAdams, David E.)
8/4/2008: Changed equations from images to Hot_Eqn. (McAdams, David E.)
6/6/2008: Initial version. (McAdams, David E.)