Ratio
Pronunciation: /ˈreɪ.ʃoʊ/ ExplainA ratio is used to compare two quantities, or to give a number that can be used to convert one unit of measure to a different, related unit of measure. For example, in 2010, there are about 307,000,000 people in the United States. Of these, about 3,000,000 live in Mississippi. The ratio of the number of people in Mississippi to the number of people in the United states is 3,000,000:307,000,000 ≈ 3:307 ≈ 1:101. This means that about 1 out of every 100 people in the United States lives in Mississippi. When comparing a part to a whole, a ratio is sometimes called a proportion.
You can also compare different things using a ratio. For example, extrapolating from existing data, there are about 120 million cats in the United States. The ratio of cats to humans is 120,000,000 to 307,000,000. 120,000,000:307,000,000 ≈ 120:307 ≈ 1:2.6. There is about one cat for every 2.6 people in the United States.
Ratios are often expressed as percentages. A percentage is a portion out of 100. 1 out of 100 is 1 percent.
A ratio can also be expressed as a real number, also called a rate. For example, if 1 gallon of gas costs $4.50, the ratio of dollars to gallons is $4.50:1. This is called the price per gallon. In this case, the price per gallon is written as $4.50/gal rather than as a ratio.
Ratios are used through math. Some of the ratios that are used are:
- Numbers
- Rational Numbers - A real number that can be expressed exactly as the ratio of two integers.
- Algebra
- Variation: - In variation, one variable differs from another by a constant ratio. The ratio is called the constant of variation.
- Geometric series - In a geometric series, each term is multiplied by a constant ratio to get the next term.
- Conversion factor - A conversion factor is a ratio used to convert one unit of measure to a related unit of measure.
- Rational expression - A rational expression is an expression that contains one or more ratios of polynomials.
- Ratio test - A test for convergences of series that uses the ratio of a term to the term before it.
- Geometry
- Trigonometric ratio - A trigonometric ratio is a ratio of the lengths of two sides of a right triangle.
- Golden Section - A golden section is the ratio that divides a line segment into two parts such that the ratio of the length of the whole to the length of the larger segment is the same as the ratio of the length of the larger segment to the smaller segment.
- Pi π - Pi is the constant ratio of the circumference of a circle to the diameter of the circle.
- Similarity ratio - The ratio of corresponding sides of similar geometric figures is constant.
- Dilation ratio - A dilation ratio tells how much bigger or smaller a dilation transformation will make an object.
- Cartography (maps)
- Map scale - A map scale is the ratio of a unit of measure on the map to the same unit of measure for the thing being mapped.
- Shopping
- Price - All prices are ratios. Usually a price tells how much for 1 unit. Sometimes a price is how much for a pound or a kilogram. Sometimes a price is something like '3 for $5'.
Converting a word problem to a ratio
Some of the keys to solving ratio word problems are:
- Make sure quantities are the same units.
- Write all ratios as fractions
The steps to solving ratio word problems are:
- Assign variables to unknown quantities
- Write one or more equations using fractions for ratios.
- Solve the equation(s).
- Convert the answer into words.
Example 1: A box of chocolates contains raspberry cremes and strawberry cremes in a ratio of 2:3. There are 10 raspberry cremes. How many strawberry cremes are in the box?
- Assign variables - The unknown is the number of strawberry cremes. Let x be the number of strawberry cremes in a box.
- Write an equation -
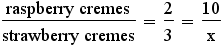 .
. - Solve the equation
- Cross multiply:
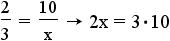 .
. - Simplify multiplication:
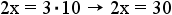 .
. - Divide both sides by 2:
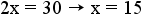 .
.
- Cross multiply:
- Convert the answer into words - There are 15 strawberry cremes in a box.
Example 2: The ratio of boys to girls in a class is 5:6. There are 33 students in the class. How many are girls?
- Assign variables - The unknowns are the number of boys and the number of girls. Let b be the number of boys and g be the number of girls.
- Write equations -
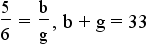 ,
,
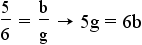 .
. - Solve the equations
- Cross multiply:
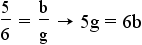 .
. - Solve for g by dividing both sides of the equation by 5:
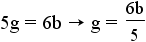 .
. - Substitute
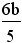 for g
in the second equation:
for g
in the second equation: 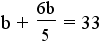
- Change the b to the common denominator of 5:
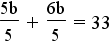 .
. - Combine the like fractions:
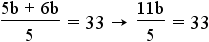 .
. - Clear the fraction by multiplying both sides of the equation by 5:
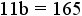 .
. - Divide both sides of the equation by 11:
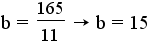 .
. - Substitue 15 for b in the second equation:
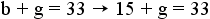 .
. - Subtract 15 from both sides of the equation:
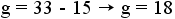 .
.
- Cross multiply:
- Convert the answer into words: There are 18 girls in the class.
References
- McAdams, David E.. All Math Words Dictionary, ratio. 2nd Classroom edition 20150108-4799968. pg 150. Life is a Story Problem LLC. January 8, 2015. Buy the book
Cite this article as:
McAdams, David E. Ratio. 4/30/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/r/ratio.html.Image Credits
- All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Revision History
4/30/2019: Changed equations and expressions to new format. (McAdams, David E.)12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
12/4/2018: Removed broken links, updated license, implemented new markup. (McAdams, David E.)
8/7/2018: Changed vocabulary links to WORDLINK format. (McAdams, David E.)
1/5/2011: Initial version. (McAdams, David E.)
- Navigation
- Home
- Contents
-
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z - Teacher Aids
- Classroom Demos
- How To
- LIASP
- LIASP Home
- Conditions of Use
- Privacy Policy
- Donate to LIASP
- Help build this site
- About LIASP
- Contact LIASP
All Math Words Encyclopedia is a service of
Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License