How to Construct a Circle From 3 Points

Click on the blue points and drag them to change the figure. Manipulative 1 - How to construct a circle from 3 points using Geogebra Created with GeoGebra.

A circle can be constructed from 3 non-collinear points. Step Construction Justification 1 Construct lines segments AB and BC. Euclid. Elements. Book 1. Proposition 1. To draw a straight line from any point to any point. 2 Construct the perpendicular bisectors of line segments AB and BC. Euclid. Elements. Book 1. Proposition 10. To bisect a given finite straight line. 3 Mark the intersection of the two perpendicular bisectors as M. 4 Construct a circle with center at M and radius MA. Euclid. Elements. Book 1. Postulate 3. To describe a circle with any center and radius.

Proof of Construction

Step	Figure	Justification
1		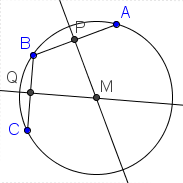Start with the completed construction. I say that the circle ABC is a circle that passes through points A, B, and C.
2		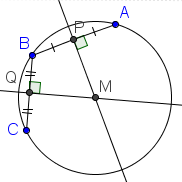By the definition of a perpendicular bisector, the perpendicular bisectors PM and QM divide segments AB and BC into two equal parts and are perpendicular to AB and BC.
3		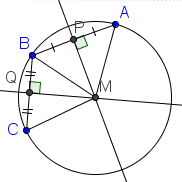Construct segments AM, BM, and CM. See Euclid. Elements. Book 1. Proposition 1. To draw a straight line from any point to any point.
4		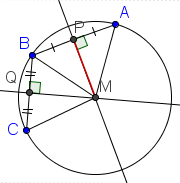Since AP = BP AND ∠APM=∠BPM, and PM is in common, by angle-side-angle congruence, ΔAPM=ΔBPM.
5		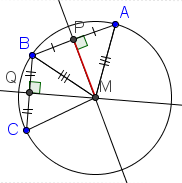Since ΔAPM = ΔBPM, line segment AM = BM.
6		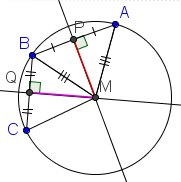Since BQ = CQ AND ∠BQM=∠CQM, and QM is in common, by angle-side-angle congruence, ΔBQM = ΔCQM.
7		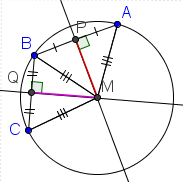Since ΔBQM=ΔCQM, line segment BM = CM.
8		By common notion 1, since AM = BM and BM = CM, then AM = CM. Since AM = BM = CM, points A, B, and C are equidistant from M. So a circle with center at point M and radius AM passes through B and C. Q.E.D..
Table 2: Proof of construction.

More Information

• Euclid of Alexandria. Elements. Clark University. 9/6/2018. https://mathcs.clarku.edu/~djoyce/elements/elements.html.

Cite this article as:

McAdams, David E. How to Construct a Circle From 3 Points. 4/22/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/h/htconstructcirclefrm3pnts.html.

Image Credits

• All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Revision History

4/22/2019: Update equations and expressions to new format. (McAdams, David E.)
7/16/2018: Removed broken links, updated license, implemented new markup, implemented new Geogebra protocol. (McAdams, David E.)
5/5/2010: Initial version. (McAdams, David E.)