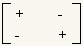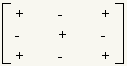Laplace Expansion

Pronunciation: /laˈplas ɪkˈspæn.ʃən/ Explain

Laplace expansion is an algorithm for finding the determinant of a matrix. Laplace expansion is also called expansion by minors and expansion by cofactors. The Laplace expansion is named after French mathematician Pierre-Simon Laplace (1749-1827).

To find a determinant of a matrix by Laplace expansion:

  • Select any row or column of the matrix;
  • Find the minor of each element in the selected row or column;
  • Add or subtract each element multiplied by the its cofactor.
The formula for Laplace expansion of a n×n matrix A is:
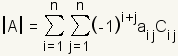The determinant of matrix A is equal to the sum for i = 1 to k of the sum for j - 1 to k of (-1)^(i+j)*a sub i,j * M sub i,j
where aij is an element of the matrix and Cij is the cofactor of element aij.

The minor of an element of a matrix is the square matrix formed out of the matrix by excluding the row and column of the element. See figure 1.

The cofactor of an element of a matrixis the determinant of the minor of that element.

Whether an element and its cofactor are added to or subtracted from the result depends on the position of the element in the matrix. Figures 2, 3, and 4 show whether a particular element is added or subtracted.

To build the equation for Laplace expansion, multiply each element from the selected row or column by its cofactor and apply the sign. Assume, for example, column 3 is selected. The equation then is: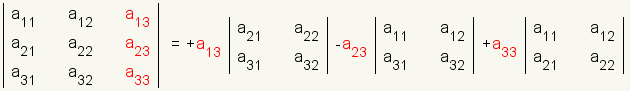

Determinant of 3x3 matrix: row 1: a11, a12, red a13; row 2: a21, a22, red a23; row 3: a31, a32, red a33; is equal to a31*determinant of 2x2 matrix: row 1: a21, a22; row 2: a31, a23 plus a32 * the determinant of 2x2 matrix row 1: a11, a12; row 2: a31, a32; plus a33 times the determinant of 2x2 matrix row1: a11, a12, row 2: a21, a22.

For 3x3 matrix: row 1: a11, a12, a13, row 2: a21, a22, a23, row 3: a31, a32, a33; the cofactor of element a12 is array: row1: a21, a23; row 2: a31, a33; the cofactor of element a21 is array: row1: a12, a13; row 2: a32, a33; the cofactor of element a33 is array: row1: a11, a12; row 2: a21, a22;
Figure 1: Minors of a 3×3 matrix.

2x2 matrix: row 1: +, -; row 2: -, +
Figure 2: Signs of cofactors for a 2×2 matrix.

3x3 matrix: row 1: +, -, +; row 2: -, +, -; row 3: +, -, +;
Figure 3: Signs of cofactors for a 3×3 matrix.

4x4 matrix: row 1: +, -, +, -; row 2: -, +, -, +; row 3: +, -, +, -; row 4: -, +, -, +;
Figure 4: Signs of cofactors for a 4×4 matrix.

Example

\
StepFigureDescription
13x3 Matrix A = row 1: 1, 3, -2; row 2: 2, 0, -2; row 3: 3, -1, -1.Find the determinant of 3x3 matrix A by cofactor expansion.
23x3 Matrix = row 1: 1, 3, -2; row 2: 2, 0, -2; row 3: 3, -1, -1. Row 2 is highlighted. Select a row or column to expand. Since element a22 is zero, it makes calculations easier. Row 2 is selected.
3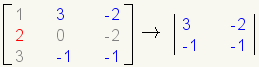3x3 Matrix = row 1: 1, blue 3, blue -2; row 2: red 2, 0, -2; row 3: 3, blue -1, blue -1 gives cofactor 2x2 matrix row 1: 3, -2; row 2: -1, -1. Start with element a21. Find the cofactor of a21.
4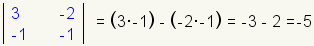The determinant of 2x2 matrix = row 1: 3, -2; row 2: -1, -1 = (3*-1)-(-2*-1) = -3 - 2 = -5 Calculate the value of the cofactor of a21.
53x3 Matrix = row 1: blue 1, 3, blue -2; row 2: 2, red 0, -2; row 3: blue 3, -1, blue -1. Since a22 is zero, it is not necessary to calculate the value of the cofactor of a22 since 0 · x = 0.
6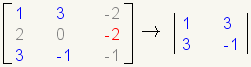3x3 Matrix = row 1: blue 1, blue 3, -2; row 2: 2, 0, red -2; row 3: blue 3, blue -1, -1 gives cofactor 2x2 matrix row 1: 3, -2; row 2: -1, -1. Now find the cofactor of element a23.
7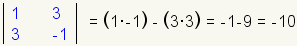The determinant of 2x2 matrix = row 1: 1, 3; row 2: 3, -1 = (1*-1)-(3*3) = -1 - 9 = -10 Calculate the value of the cofactor of a23.
8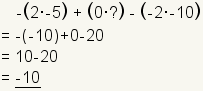-(2*-5)+(0*?)-(-2*10) = -(-10)+0-20 = 10-20 = -10}Use the cofactor equation to find the determinant.
Table 1: Laplace expansion.

References

  1. cofactor. merriam-webster.com. Encyclopedia Britannica. Merriam-Webster. Last Accessed 8/31/2018. http://www.merriam-webster.com/dictionary/cofactor. Buy the book
  2. Ferrar, W. L.. Algebra. 2nd edition. pp 28-40. www.archive.org. Oxford University Press. 1960. Last Accessed 8/31/2018. http://www.archive.org/stream/algebra032104mbp#page/n45/mode/1up/search/laplace. Buy the book
  3. Doherty, Robert E.; Keller,Ernest G.. Mathematics Of Modern Engineering Vol I. pp 58-60. www.archive.org. John Wiley & Sons, Inc.. October 1949. Last Accessed 8/31/2018. http://www.archive.org/stream/mathematicsofmod029509mbp#page/n83/mode/1up/search/laplace. Buy the book
  4. Jeffrey, Alan; Dai, Hui Hui. Handbook of Mathematical Formulas and Integrals. 4th edition. pp 51-53. Academic Press. February 1, 2008. Last Accessed 8/31/2018. Buy the book

More Information

  • McAdams, David E.. Matrix. allmathwords.org. All Math Words Encyclopedia. Life is a Story Problem, LLC.. 8/31/2018. https://www.allmathwords.org/en/m/matrix.html.

Cite this article as:

 McAdams, David E. Laplace Expansion. 4/23/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/l/laplaceexpansion.html.

Image Credits

Revision History

4/23/2019: Changed equations and expressions to new format. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
8/31/2018: Removed broken links, updated license, implemented new markup. (McAdams, David E.)
8/7/2018: Changed vocabulary links to WORDLINK format. (McAdams, David E.)
3/7/2010: Added "References". (McAdams, David E.)
1/8/2009: Initial version. (McAdams, David E.)

All Math Words Encyclopedia is a service of Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License