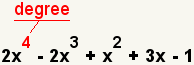Polynomial

Pronunciation: /ˌpɒl.əˈnoʊ.mi.əl/ Explain
3x3 + x2 + 4
Figure 1: A polynomial

3x2 + 2x + 4
Figure 2: Polynomial in standard form.

2x + 3x2 + 4
Figure 3: Polynomial not in standard form.

(x + 1)(x - 2)(x2 + x + 7)
Figure 4: Polynomial in factored form.

A polynomial is an expression with one or more terms. Each term has a coefficient and one or more variables each with an integer exponent.

The standard form of a polynomial is the highest exponent first, followed by the next highest, and so on down to the constant term. See figures 2 and 3. The factored form of a polynomial is a polynomial expressed as factors with the least degree. A factor of the least degree is a number, a first degree polynomial, or a second degree polynomial with no real roots.

Article Index

Terms of Polynomials
Degree of a Polynomial
End Behavior of Polynomials
Roots of a Polynomial
Special Polynomials
Addition and Subtraction of Polynomials
Multiplication of Polynomials
Division of Polynomials

Terms of Polynomials

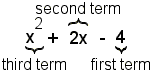The polynomial x^2+2x-4. The first term is x^2. The second term is 2x. The third term is -4.
Figure 5: Polynomial terms
3x2 + 2
Figure 6: Polynomial terms

Each term of a polynomial is separated from other terms by addition or subtraction. In the polynomial in figure 5, the first term is -4. The second term is 2x. The third term is x2.

Each term of a polynomial has a coefficient. The coefficient can be any real number. For the term x2 the coefficient is 1. The property of multiplying by 1 states that 1 · x2 = x2, so the 1 is implied. The following real numbers can be coefficients: 1/2, 0.3, π, log210.

Notice that a coefficient may be 0. According to the property of multiplying by 0 anything times 0 is 0. In figure 6, the term x does not appear. This is because it has a term of 0. This term can also be written 0x. Because 0x = 0, this term is not normally written.

Each term has a variable with an integer exponent. In the case of the term 2x in figure 5, the exponent of 1 is implied. This is because x1 = x.

The constant term in figure 5 is -4. If the constant term is 0, it is not usually written. If the polyomial has only a constant term, has no terms with variables, it is considered a degenerate polynomial.

Check Mark Understanding Check

Click on the check box of the answer you think is correct.
  1. Is 3x2 - 2x + 1 a polynomial?
    no answercorrect YesYes. Correct. 3x2 - 2x + 1 is a polynomial. Each term has a real coefficient and a variable with an integer exponent.
    no answerincorrect NoNo. Incorrect. 3x2 - 2x + 1 is a polynomial. Each term has a real coefficient and a variable with an integer exponent.
  2. Is x + 1 a polynomial?
    no answercorrect YesYes. Correct. x + 1 is a polynomial. Each term has a real coefficient and a variable with an integer exponent.
    no answerincorrect NoNo. Incorrect. x + 1 is a polynomial. Each term has a real coefficient and a variable with an integer exponent.
  3. Is -2x1/2 + 3x - 4 a polynomial?
    no answerincorrect YesYes. Incorrect. In the term -2x1/2, the exponent 1/2 is not an integer.
    no answercorrect NoNo. Correct. In the term -2x1/2, the exponent 1/2 is not an integer.
  4. Is 1/2x2 - 8x + 1 a polynomial?
    no answercorrect YesYes. Correct. 1/2x2 - 8x + 1 is a polynomial. Each term has a real coefficient and a variable with an integer exponent.
    no answerincorrect NoNo. Incorrect. 1/2x2 - 8x + 1 is a polynomial. Each term has a real coefficient and a variable with an integer exponent.
  5. Is -5x2 + 4x a polynomial?
    no answercorrect YesYes. Correct. -5x2 + 4x is a polynomial. Each term has a real coefficient and a variable with an integer exponent. Note that the constant term is 0, and so is omitted.
    no answerincorrect NoNo. Incorrect. -5x2 + 4x is a polynomial. Each term has a real coefficient and a variable with an integer exponent. The constant term is 0, and so is omitted.
  6. Is -x2.3 + 1 a polynomial?
    no answerincorrect YesYes. Incorrect. -x2.3 + 1 is not a polynomial. The exponent on the term -x2.3 is not an integer.
    no answercorrect NoNo. Correct. -x2.3 + 1 is not a polynomial. The exponent on the term -x2.3 is not an integer.
  7. Is 3 a polynomial?
    no answercorrect YesYes. Correct. A constant can be considered a degenerate polynomial. This polynomial can be written 3x0, since x0 = 1.
    no answerincorrect NoNo. Incorrect. A constant can be considered a degenerate polynomial. This polynomial can be written 3x0, since x0 = 1.

Degree of a Polynomial

The polynomial 2x^4-2x^3+x^2+3x-1 is degree 4.
Figure 7 - Degree 4 polynomial

The degree of a single variable polynomial is the highest exponent. In figure 7, the highest exponent is 4, so the degree of the polynomial is 4.

Check Mark Understanding Check

Click on the check box of the answer you think is correct.
  1. What is the degree of the polynomial 3x2 - 2x + 1?
    no answerincorrect 00: Incorrect. There is a term with an exponent of 0, but the highest exponent is 2, so the degree of the polynomial is 2.
    no answerincorrect 11: Incorrect. There is a term with an exponent of 1, but the highest exponent is 2, so the degree of the polynomial is 2.
    no answercorrect 22: Correct. The highest exponent is 2, so the degree of the polynomial is 2.
    no answerincorrect 33: Incorrect. There is no term with an exponent 3. The highest exponent is 2, so the degree of the polynomial is 2.
    no answerincorrect 44: Incorrect. There is no term with an exponent 4. The highest exponent is 2, so the degree of the polynomial is 2.
    no answerincorrect 55: Incorrect. There is no term with an exponent 5. The highest exponent is 2, so the degree of the polynomial is 2.
  2. What is the degree of the polynomial -3x4 + 2x3 - 2x + 1?
    no answerincorrect 00: Incorrect. There is a term with an exponent 0, but the highest exponent is 4, so the degree of the polynomial is 4.
    no answerincorrect 11: Incorrect. There is a term with an exponent 1, but the highest exponent is 4, so the degree of the polynomial is 4.
    no answerincorrect 22: Incorrect. There is no term with an exponent 2. The highest exponent is 4, so the degree of the polynomial is 4.
    no answerincorrect 33: Incorrect. There is a term with an exponent 3, but the highest exponent is 4, so the degree of the polynomial is 4.
    no answercorrect 44: Correct. The highest exponent is 4, so the degree of the polynomial is 4.
    no answerincorrect 55: Incorrect. There is no term with an exponent 5. The highest exponent is 4, so the degree of the polynomial is 4.
  3. What is the degree of the polynomial 6?
    no answercorrect 00: Correct. A constant can be considered a polynomial of degree 0.
    no answerincorrect 11: Incorrect. A constant can be considered a polynomial of degree 0.
    no answerincorrect 22: Incorrect. A constant can be considered a polynomial of degree 0.
    no answerincorrect 33: Incorrect. A constant can be considered a polynomial of degree 0.
    no answerincorrect 44: Incorrect. A constant can be considered a polynomial of degree 0.
    no answerincorrect 55: Incorrect. A constant can be considered a polynomial of degree 0.

Degree of Multi-variable Polynomials

The degree of a multi-variable polynomial is the highest sum of the exponents on the variables. For example, the polynomial x2y + 3x2y3 has a degree of 5: (2 + 3 = 5).

End Behavior of Polynomials

blank spacePositive TermNegative Term
Even DegreeGraph of x^2+3x-1 with both ends of the polynomial pointing upwards.Graph of -x^2+3x+1 with both ends of the polynomial pointing downwards.
Odd DegreeGraph of 2x^3-x^2-5x-1 with the left end pointing down and the right end pointing up.Graph of -2x^3-x^2+5x-1 with the left end of the polynomial pointing upwards and the right end pointing downwards.
Table 1: End behavior of polynomials.

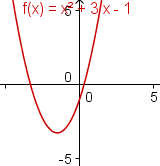
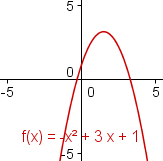
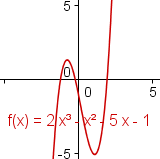
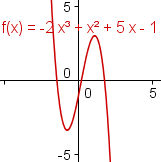
As the argument of a polynomial moves towards positive or negative infinity, the value of the polynomial also moves towards positive or negative infinity. This is called the end behavior of the polynomial.

For polynomials with even degree, both ends of the polynomial point in the same direction. For polynomials with odd degree, the ends of the polynomial point in different directions. Polynomials with a positive term of the highest degree go up on the right. Polynomials with a negative term of the highest degree go down on the right.

Click on the points on the blue siders and drag them to change the figure.

Manipulative 1 - End Behavior of a Polynomial Created with GeoGebra.

If the leading sign is positive, the right side of the polynomial goes towards infinity. If the leading sign is negative, the right side of the polynomial goes towards negative infinity. If the degree is even, the left side of the polynomial goes towards the same value as the right side. If the degree of the polynomial is odd, the left side of the polynomial goes towards the opposite value of the right side.

Roots of a Polynomial

The roots of a polynomial are the values the variable of a polynomial can take when the polynomial is set equal to zero. A root of a polynomial can also be called a zero of a polynomial. For example, take the binomial x - 3. Setting the binomial to zero gives x - 3 = 0. Solving for x gives x = 3. So 3 is a zero of the binomial x - 3. One can also say that 3 is a root of the binomial x - 3. For more information on finding roots of polynomials, see Factoring Polynomials.

Special Polynomials

A polynomial of degree 2 is called a quadratic. A polynomial of degree 3 is called a cubic. A polynomial with exactly 2 terms is called a binomial.

Addition and Subtraction of Polynomials

Click on the points on the sliders and drag them to change the figure.

Manipulative 2 - Addition of Polynomials Created with GeoGebra.

When adding two polynomials, like terms are added together. The easiest way to do this is to put the polynomials in standard form, one under the other. Addition of polynomials is associative: P( x ) + [Q(x) + R(x)] = [P(x) + Q(x)] + R(x)]. Addition of polynomials is commutative: P( x ) + Q(x) = Q( x ) + P( x ).

Click on the red and green points in manipulative 1 and drag them to change the figure.

Discovery

  1. What shape does h( x ) make if >a1 = -a2?
    Click for hint.
  2. If f( x ) opens upward ( a1 > 0 ) and g( x ) opens downward (a2 < 0), in which direction will h( x ) open?
    Click for hint.

Examples

StepEquation(s)Description
1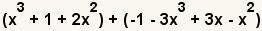(x^3+1+2x^2)+(-1-3x^3+3x-x^2)These are the polynomials to add.
2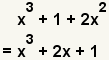x^3+1+2x^2=x^3+2x^2+1Put the first polynomial in standard form, from the highest degree term to the lowest.
3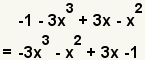-1-3x^3+3x-x^2=-3x^3-x^2+3x-1Put the second polynomial in standard form, from the highest degree term to the lowest.
4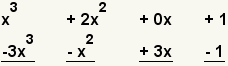(x^3+2x^2+1)+(-3x^3-x^2+3x-1)=-2x^3+x^2+3x+0Line up the polynomials, one under the other. Since the first polynomial does not have an 'x' term, fill in 0x.
5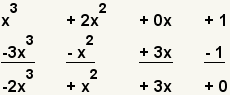(x^3+1+2x^2)+(-1-3x^3+3x-x^2)=-2x^3+x^2+3x+0 Add the terms vertically.
6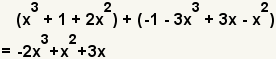(x^3+1+2x^2)+(-1-3x^3+3x-x^2)=-2x^3+x^2+3xThis is the result.
Example 1

Subtraction of polynomials is like addition of polynomials. Instead of adding like terms, one subtracts like terms. Subtraction of polynomials is associative: P( x ) - [ Q( x ) - R( x )] = [P( x ) - Q( x )] - R( x )]. Subtraction of polynomials is not commutative: P( x ) - Q( x ) ≠ Q( x ) - P( x ).

StepEquation(s)Description
1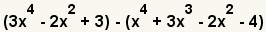These are the polynomials to subtract.
2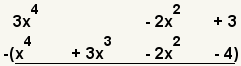Put the polynomials in standard form, one under the other.
3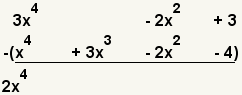Subtract the highest degree terms. 3x4 - x4 = 2x4.
4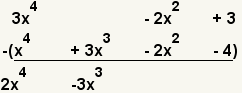Subtract the next highest degree terms. 0x3 - 3x3 = -3x3.
5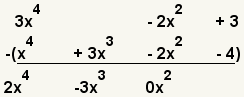Repeat the process with the next terms. -2x2 - -2x2 = 0x2.
6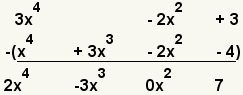Repeat the process with the next terms. 3 - -4 = 7.
7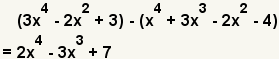This is the result.
Example 2

Multiplication of Polynomials

To multiply polynomials, multiply each of the terms of the first polynomial by each of the terms of the second polynomial. Then add like terms. Multiplication of polynomials is associative: P( x ) · [ Q( x ) · R(x)] = [ P(x) · Q( x )] · R( x )]. Multiplication of polynomials is commutative: P( x ) · Q( x ) = Q( x ) · P( x ).

Examples

StepEquations(s)Description
1(x^3+2x^2+1)*(3x^3-x^2+3x-1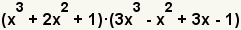)These are the polynomials to multiply.
2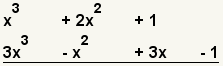(x^3+2x^2+1)*(3x^3-x^2+3x-1)Line the polynomials one under the other.
3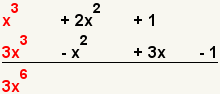(x^3+2x^2+1)*(3x^3-x^2+3x-1)=3x^6 ...Multiply the first terms of the polynomials.
4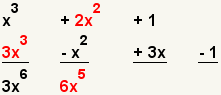(x^3+2x^2+1)*(3x^3-x^2+3x-1)=3x^6-2x^4 ...Multiply the second term of the first polynomial with the first term of the second polynomial.
5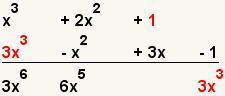(x^3+2x^2+1)*(3x^3-x^2+3x-1)=3x^6-2x^4 ...Multiply the third term of the first polynomial with the first term of the second polynomial.
6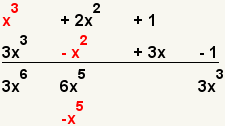(x^3+2x^2+1)*(x^3+2x^2=1)Multiply the first term of the first polynomial with the second term of the second polynomial.
7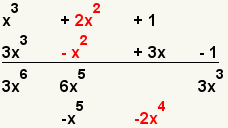(x^3+2x^2+1)*(x^3+2x^2=1)Multiply the second term of the first polynomial with the second term of the second polynomial.
8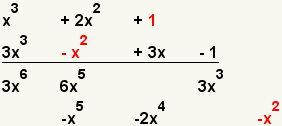(x^3+2x^2+1)*(x^3+2x^2=1)Multiply the third term of the first polynomial with the second term of the second polynomial.
9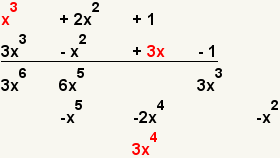(x^3+2x^2+1)*(x^3+2x^2=1)Multiply the first term of the first polynomial with the third term of the second polynomial.
10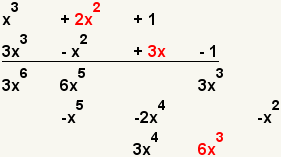(x^3+2x^2+1)*(x^3+2x^2=1)Multiply the second term of the first polynomial with the third term of the second polynomial.
11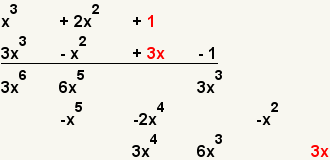(x^3+2x^2+1)*(x^3+2x^2=1)Multiply the third term of the first polynomial with the third term of the second polynomial.
12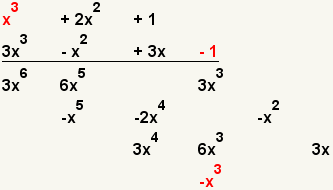(x^3+2x^2+1)*(x^3+2x^2=1)Multiply the first term of the first polynomial with the forth term of the second polynomial.
13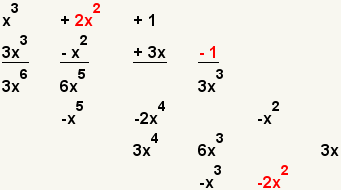(x^3+2x^2+1)*(x^3+2x^2=1)Multiply the second term of the first polynomial with the forth term of the second polynomial.
14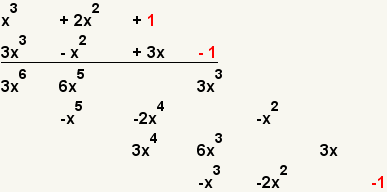(x^3+2x^2+1)*(x^3+2x^2=1)Multiply the third term of the first polynomial with the forth term of the second polynomial.
15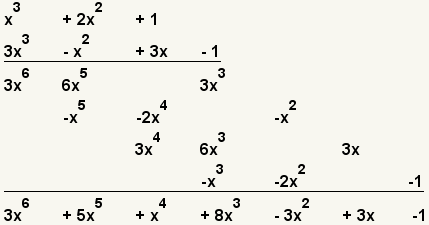(x^3+2x^2+1)*(x^3+2x^2=1)Add all the like terms.
16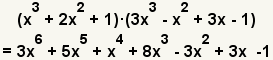(x^3+2x^2+1)*(x^3+2x^2=1)=3x^6+5x^5+x^4+8x^3-3x^2+3x-1This is the result.
Example 3

Division of Polynomials

Division of polynomials is a lot like long division. Instead of dealing with digits, one deals with the terms of the polynomial. Division of polynomials is associative: P( x ) ÷ [ Q( x ) ÷ R( x )] = [ P( x ) ÷ Q( x )] ÷ R( x )]. Division of polynomials is not commutative: P( x ) ÷ Q( x ) ≠ Q( x ) ÷ P( x ).

Examples

StepEquations(s)Description
1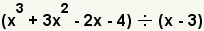(x^3+3x^2-2x-4)/(x-3)In this example, we will divide the polynomial
x3 + 3x2 - 2x - 4 by x - 3.
2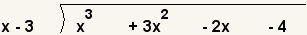x-3 goes in to x^3+3x^2-2x-4Arrange the polynomials like long division with the divisor on the left and the dividend on the right.
3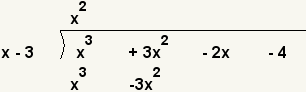(x^3+2x^2+1)*(3x^3-x^2+3x-1)What value times x equals x3? x · x2 = x3. So put x2 on the top and the product of x2 and x - 3 on the bottom. x2 · (x - 3) = x3 - 3x2.
4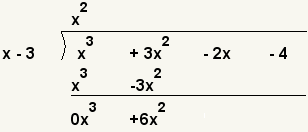(x^3+2x^2+1)*(3x^3-x^2+3x-1)Subtract x3 - 3x2 from the dividend. ( x3 + 3x2 ) - ( x3 - 3x2) = 0x3 + 6x2.
5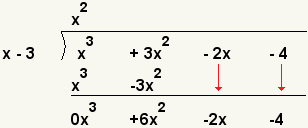(x^3+2x^2+1)*(3x^3-x^2+3x-1)Bring down the rest of the terms.
6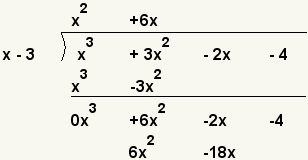(x^3+2x^2+1)*(3x^3-x^2+3x-1)What value times x equals 6x2? x · 6x = 6x2. So put 6x on the top and the product of 6x and x - 3 on the bottom. 6x · (x - 3) = 6x2 - 18x.
7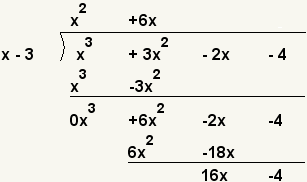(x^3+2x^2+1)*(3x^3-x^2+3x-1)Subtract 6x2 - 18x from the last difference. ( 6x2 - 2x ) - ( 6x2 - 18x ) = 0x2 + 16x. Bring down the last term.
8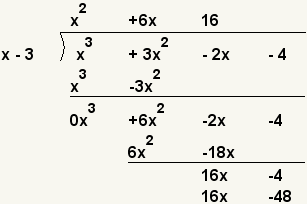(x^3+2x^2+1)*(3x^3-x^2+3x-1)What value times x equals 16x? x · 16 = 16x. So put 16 on the top and the product of 16 and x - 3 on the bottom. 16 · ( x - 3 ) = 16x - 48.
9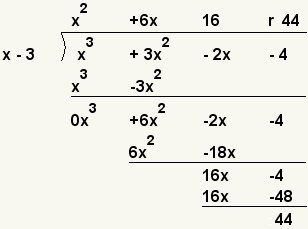(x^3+2x^2+1)*(3x^3-x^2+3x-1)Subtract 6x - 48 from the last difference. ( 16x - 4 ) - ( 16x - 48) = 44.
10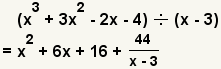(x^3+2x^2+1)*(3x^3-x^2+3x-1)Since x - 3 can not go evenly into 44, 44 is the remainder.
Example 4

Synthetic Division

See Synthetic Division.

Factoring Polynomials

See Factoring Polynomials.

References

  1. McAdams, David E.. All Math Words Dictionary, polynomial. 2nd Classroom edition 20150108-4799968. pg 142. Life is a Story Problem LLC. January 8, 2015. Buy the book
  2. Keigwin, H. W.. Principles of Elementary Algebra. pg 4. www.archive.org. Ginn & Company. 1886. Last Accessed 12/3/2018. http://www.archive.org/stream/principlesofelem00dupurich#page/4/mode/1up/search/polynomial. Buy the book
  3. Bettinger, Alvin K. and Englund, John A.. Algebra and Trigonometry. pg 17-25,61-62. www.archive.org. International Textbook Company. January 1963. Last Accessed 12/3/2018. http://www.archive.org/stream/algebraandtrigon033520mbp#page/n18/mode/1up. Buy the book

More Information

  • McAdams, David E.. Degree of an Equation. allmathwords.org. All Math Words Encyclopedia. Life is a Story Problem LLC. 3/12/2009. https://www.allmathwords.org/en/d/../d/degreeequation.html.

Cite this article as:

 McAdams, David E. Polynomial. 4/28/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/p/polynomial.html.

Image Credits

Revision History

4/28/2019: Changed equations and expressions to new format. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
12/1/2018: Removed broken links, updated license, implemented new markup, updated geogebra app. (McAdams, David E.)
8/7/2018: Changed vocabulary links to WORDLINK format. (McAdams, David E.)
2/10/2009: Rewrote section on end behavior. (McAdams, David E.)
2/6/2009: Added sections on addition, multiplication and division of polynomials. (McAdams, David E.)
1/29/2009: Added section on roots of polynomials. (McAdams, David E.)
1/20/2009: Added reference to Factorizing Polynomials. (McAdams, David E.)
12/17/2008: Added 'End Behavior of Polynomials'. (McAdams, David E.)
5/1/2008: Added info for multiple variable polynomials and standard form. (McAdams, David E.)
4/4/2008: Initial version. (McAdams, David E.)

All Math Words Encyclopedia is a service of Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License