Ã?ngulo
Un ángulo es la
rotación
entre dos rectas,
semirectas
o rectas segmentos
de intersección.
 |
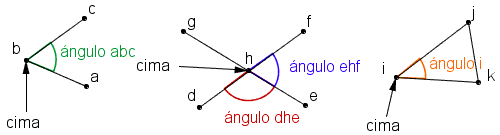| Cuadro 1: Varios ángulos |
La vértice de un ángulo es el punto
de la intersección
de las rectas. En el cuadro 1, las vértices son los puntos b, h, e i.
Dos ángulos son equiángulos si las
medidas de los ángulos son iguales.
Ã?ndice del artÃculo
Medida de un ángulo
La medida de un ángulo se hace en términos de medida de un circunferencia completo.
La unidad de medida para un ángulo es grado sexagesimal, radianes o, en casos raros,
grados centesimal.
Grado sexagesimal
|
| | El manipulante 1: Ã?ngulo del grado. Creado con GeoGebra. |
|
El grado sexagesimal es la más vieja unidad de medida
para un ángulo. Los grados son denotados por un pequeño circunferencia (°) o el
grado. Por definición, un circunferencia
completo es 360°. El significa que un ángulo que es 1/4 de un circunferencia es 360°/4,
o el 90°. Vea el manipulante 1. Chascar encendido el punto azul en el manipulante 1 y
arrastrarlo para cambiar la figura.
 Cheque de comprensión
Calcule la respuesta al problema y anótela. Entonces chasque encendido las
palabras azules y amarillas para ver la respuesta correcta.
- La medida del grado de un ángulo que sea 1/3 de un circunferencia es:
Chasque para ver la respuesta. 360/3 = 120
- La medida del grado de un ángulo que sea 1/17 de un circunferencia es:
Chasque para ver la respuesta. 360/17 ≈ 21.18
|
Radián
|
| | El manipulante 2: Ã?ngulo en radianes. Creado con GeoGebra. |
|
Al medir ángulos, el radián es particularmente útil. Se
define un radián como el ángulo hecho con una longitud de arco de 1 en un
circunferencia de unidad.
Esto significa que la longitud de un arco de 1 radián es igual que la longitud del
radio del circunferencia. Vea el manipulante 2. Hay los radianes
2π
en un circunferencia completo. Un ángulo que es 1/5 de un circunferencia
es el 2π/5 ≈ 1.26 radianes. La abreviatura para el radián es
rad. Chasque encendido el punto azul en el manipulante 1
y arrástrelo para cambiar la figura.
Una razón la medida de radianes es asà que útil tiene que hacer con la ecuación
famosa de Euler que relaciona la exponenciación con trigonometrÃa usando
números complejos:
eiθ = cos(θ) + i·sin(θ). Esta ecuación
trabaja si y solamente si del ángulo se mide en radianes.
Cheque de comprensión
Calcule la respuesta al problema y anótela. Entonces chasque encendido
las palabras azules y amarillas para ver la respuesta correcta.
- La medida del radián de un ángulo que sea 1/3 de un circunferencia es:
Chasque para ver la respuesta. 2·π/3 ≈ 2.09
- La medida del radián de un ángulo que sea 1/17 de un circunferencia es:
Chasque para ver la respuesta. 2·π/17 ≈ 0.37
|
Grado centesimal
Una medida raramente usada del ángulo es grado centesimal.
Un circunferencia completo mide 400 gradians.
Clases de ángulos
|
| | El manipulante 3: Clases del ángulo. Creado con GeoGebra. |
|
Para la conveniencia en discusiones de ángulos y de la trigonometrÃa, los ángulos
se dividen en clases. La clase que un ángulo pertenece a es determinada por su medida.
El cuadro 1 demuestra las clases de ángulos y de sus medidas. Chasque encendido el
punto azul en el manipulante 1 y arrástrelo para cambiar la figura. El manipulante 1
también demuestra las clases de ángulos y de sus medidas.
|
Ã?ngulo inscrito
|
| | El manipulante 4: Ã?ngulo inscrito. Creado con GeoGebra. |
|
| | El manipulante 5: �ngulo inscrito en el diámetro de un circunferencia. Creado con GeoGebra. |
|
Un ángulo inscrito es un ángulo hecho de puntos en la
circunferencia
de un circunferencia.
Descubrimiento
- ¿Todos los ángulos inscritos son mayores que qué medida?
Tecleo para la respuesta. Todos los ángulos inscritos es mayor de cero. Mueva las puntos finales de las piernas del cierre del ángulo juntas, pero lejos de la vértice. Cuanto más cercanas las puntos finales están el uno al otro, ellos más cerca que el ángulo está a cero.
- ¿Todos los ángulos inscritos son más pequeños que qué medida?
Tecleo para la respuesta. Todos los ángulos inscritos es más pequeño que un ángulo llano. Mueva las puntos finales de las piernas del ángulo cerca de cada lado de la vértice, pero en los lados opuestos de la vértice. Cuanto más cercanas las puntos finales están a la vértice, ellos más cerca que el ángulo está a un ángulo llano.
- ¿Cómo la medida del ángulo inscrito cambia cuando solamente la vértice se mueve sin la mudanza a través de una de las puntos finales?
Tecleo para la respuesta. Si las puntos finales del ángulo inscrito se salen solamente y la vértice del ángulo inscrito se mueve, la medida del ángulo no cambia.
- ¿Cómo la medida del ángulo inscrito cambia cuando la vértice se mueve a través de una de las puntos finales?
Tecleo para la respuesta. Si la vértice se mueve a través de una de las puntos finales, el ángulo anterior y el nuevo ángulo son complementarios. Los ángulos agregan para arriba a un ángulo llano.
- ¿Si un ángulo está inscrito en el diámetro de un circunferencia, cuál es la medida del ángulo inscrito?
Tecleo para la respuesta. La medida de un ángulo inscrito en el diámetro de un circunferencia es una de ángulo llano.
|
Ã?ngulo central
|
|
|
El manipulante 6: Ã?ngulo central de un circunferencia. Creado con GeoGebra. |
|
Un ángulo central de un circunferencia es un ángulo
con la vértice en el centro del circunferencia y los otros dos puntos en la
circunferencia del circunferencia. Chasque encendido los puntos azules en el
manipulante 6 y arrástrelos para cambiar la figura.
Para un ángulo inscrito y un ángulo central con las mismas puntos finales,
la medida del ángulo inscrito es mitad de la medida del ángulo central. Chasque
encendido los puntos azules en el manipulante 7 y arrástrelos para cambiar la figura.
|
|
|
|
El manipulante 7: Relación entre los ángulos centrales e inscritos. Creado con GeoGebra. |
|
�ngulo de la rotación
Ã?ngulos complementarios
|
| | El manipulante 9: Ã?ngulos complementarios. Creado con GeoGebra. |
|
Dos ángulos son complementarios si producen un de
ángulo llano
cuando están combinados. Esto significa que el α y el β
dado de los ángulos, el α y el β son complementarios
si α + β = π/2.
Ã?ngulos suplementarios
Dos ángulos son suplementarios si producen una recta
recta cuando están combinados. Esto significa que el α y el
β dado de los ángulos, el α y el β
son suplementarios si α + β = π.
|
|
|
| | El manipulante 10: Ã?ngulos suplementarios. Creado con GeoGebra. |
|
|
Copiado de un ángulo
Un ángulo se puede copiar usando un
compás
y un borde recto.
|
| |
El manipulante 11: Copiado de un ángulo. Creado con GeoGebra. |
Ã?ngulo bisectriz
|
| |
El manipulante 12: Bisección de un ángulo. Creado con GeoGebra. |
|
Un bisectriz de un ángulo es una recta el segmento o
el semirecta que dividen un ángulo en dos ángulos congruentes.
|
Postulado de la suma del ángulo
|
| | El manipulante 13: Postulado de la suma del ángulo. Creado con GeoGebra. |
|
El postulado de la suma del ángulo indica que los
ángulos adyacentes
se pueden agregar juntos para formar un ángulo más grande. Esto es un postulado o el
axioma,
significándolo se acepta como verdad sin prueba.
|
- Varios ángulos
- ángulo de 90 grados
- 1 radián
- Ã?ngulos inscritos
- Un ángulo inscrito en un circunferencia
- Un ángulo inscrito en el diámetro de un circunferencia
- Ã?ngulo central de un circunferencia.
- Relación entre los ángulos centrales e inscritos
- Ã?ngulos complementarios
- Ã?ngulos suplementarios
- Copiado de un ángulo
- Ã?ngulo bisectriz
- Bisección de un ángulo
Más información
- ángulo. buscon.rae.es. Real Academia Española. 2009-04-09. http://buscon.rae.es/draeI/SrvltConsulta?TIPO_BUS=3&LEMA=ángulo.
Citar este artÃculo como:
�ngulo. 2009-04-03. Enciclopedia de Todas las Palabras de la Matemáticas. Life is a Story Problem LLC. https://www.allmathwords.org/es/a/angle.html.
Traducciones
créditos de imagen
- Todas las imágenes y manipulatives están por David McAdams a menos que estén indicadas de otra manera. Todas las imágenes de David McAdams son & de los derechos reservados; © Life is a Story Problem LLC y se puede reproducir para el uso educativo no comercial solamente.
La historia de revisión
2009-04-03: Traducido automáticamente por BabelFish. (babelfish.yahoo.com.)
2008-10-28: Manipulatives cambiados y algunos gráficos al geogebra (McAdams, David.)
2008-09-19: TÃtulo cambiado la '' otra información '' a '' más información '', dicitonary.com a más información (McAdams, David.)
2008-07-07: Errores corregidos del acoplamiento (McAdams, David.)
2008-04-28: Clase agregada de la palabra clave a las clasificaciones del ángulo (McAdams, David.)
2008-04-19: Revisado bisecando una tabla del ángulo para reflejar la mayorÃa del método común (McAdams, David.)
2008-03-11: Varios errores fijos del formato y del acoplamiento (McAdams, David.)
2008-02-03: �ngulo cambiado de la entidad del HTML del ángulo de la palabra (McAdams, David.)
2007-08-17: Versión inicial (McAdams, David.)
|
Este trabajo
se autoriza debajo de una
Creative Commons Attribution-Noncommercial-Share Alike 3.0 License