Ceva's Theorem

Pronunciation: /sɛvʌz ˈθɪər.əm/ Explain

Click on the blue points on the figure and drag them to change the figure. Can the figure be changed so that the product of the ratios is not equal to one? Manipulative 1 - Ceva's Theorem Created with GeoGebra.

Ceva's theorem states that; given a triangle ABC, and points D, E, and F that lie on lines AB, BC, and CA respectively, lines AE, BF, and DC are concurrent if and only if .[2] The theorem is named after Giovanni Ceva (1647-1734), who proved it his 1678 work De lineis rectis. However it was proved much earlier by Yusuf Al-Mu'taman ibn Hud (المؤتمن بالله يوسف إبن أحمد إبن هود), an eleventh-century king of Zaragoza.

Proof of Ceva's Theorem

Click on the blue dots and drag them to change the figure. Review the proof below using this diagram.

Manipulative 2 - Proof of Ceva's Theorem Created with GeoGebra.

Step	Discussion	Justification
0	Let ABC be a triangle. Let D be a point but not an endpoint on AB; E be a point but not an endpoint on BC; F be a point but not an endpoint on CA such that the segments AE, BF and CD are concurrent. Let P be the point where AE, BF and CD are concurrent.	These are the criteria.
1	Draw a line through C parallel to AB. Label this line c.
2	Extend line segment AE. Label this line e. Label the intersection of lines c and e as A'.
3	Extend line segment BF. Label this line f. Label the intersection of lines c and f as B'.
4	Angle AEB and angle A'EC are congruent.	Angles AEB and A'EC are opposite angles.
5	Angles A'CE and ABC are congruent.	Since BC is a transversal of parallel lines AB and c, angles A'CE and ABC are congruent.
6	Angles AA'C and A'AB are congruent.	Since BC is a transversal of parallel lines AB and c, angles A'CE and ABC are congruent.
7	Triangles ABE and A'CE are similar triangles.	Since AEB is congruent with A'EC, A'CE is congruent with ABC and AA'C is congruent with A'AB, triangles ABE and A'CE are similar triangles.
8	Triangles BAF and B'CF are similar triangles.	Triangles BAF and B'CF are similar by an argument similar to steps 4-6.
9	The following equalities hold: .	The ratio of one corresponding side of a similar triangles to another corresponding side are equal.
10	Now multiply the respective sides of the equations in step 10 to get 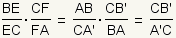.	This uses the multiplicative property of equality and the substitution property of equality.
11	Triangle ADP is similar to triangle A'CP.	Triangle ADP is similar to triangle A'CP by an argument similar to steps 4-6.
12	Triangle BDP is similar to triangle B'CP.	Triangle BDP is similar to triangle B'CP by an argument similar to steps 4-6.
13	The following equalities hold:	The ratio of one corresponding side of a similar triangles to another corresponding side are equal.
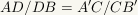
14	This gives	This uses the transitive property of equality and the multiplicative property of equality.
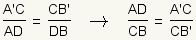
15	Multiplying the equation from step 10 with the equation from step 14 gives Q.E.D.	This uses the multiplicative property of equality.
Converse
Step	Discussion	Justification
1	Suppose that E, F, and D are points on BC, CA and AB respectively satisfying 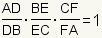.	These are the criteria.
2	Let Q be the intersection of AE with BF and D' be the intersection of CQ with AB.
3	Since AE, BF and CD' are concurrent, and .
4	Step #3 implies D = D', so AE, BF, and CD are concurrent. Q.E.D.
Table 1: Proof of Ceva's Theorem. Proof courtesy Yark. Licensed under Creative Commons Attribution 2.5 license.

References

1. McAdams, David E.. All Math Words Dictionary, Ceva's Theorem. 2nd Classroom edition 20150108-4799968. pg 32. Life is a Story Problem LLC. January 8, 2015. Buy the book
2. Godfrey, C. and Siddons, A.W.. Modern Geometry. pp 46-52. www.archive.org. Cambridge University Press. 1908. Last Accessed 6/25/2018. http://www.archive.org/stream/moderngeometry00godfrich#page/46/mode/1up/search/Ceva. Buy the book
3. Coxeter, H.M.S. and Greitzer, S.L.. Geometry Revisited. 1st edition. pp 4-6. The Mathematical Association of America. 1967. Last Accessed 6/25/2018. Buy the book

More Information

• McAdams, David E.. Cevian. allmathwords.org. All Math Words Encyclopedia. Life is a Story Problem LLC. 6/27/2018. https://www.allmathwords.org/en/c/cevian.html.

Cite this article as:

McAdams, David E. Ceva's Theorem. 4/14/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/c/cevastheorem.html.

Image Credits

• All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Revision History

4/14/2019: Updated equations and expressions to new format. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
6/25/2018: Removed broken links, updated license, implemented new markup, updated GeoGebra apps. (McAdams, David E.)
1/9/2010: Added "References". (McAdams, David E.)
11/21/2008: Initial version. (McAdams, David E.)