Proportional

Pronunciation: /prəˈpoʊr.ʃə.nl/ Explain

Two variables are proportional if they have a common ratio.

An example of proportional values is the price of gasoline. Signs advertising the price of gas give it in dollars per gallon. The price posted is the common ratio. To calculate the total price, multiply the price per gallon times the number of gallons. Given a price of $3.00 per gallon, This can be expressed as a function t( g ) = 3g, where g is the number of gallon of gas and t( g ) is the total price of the gas. The graph in figure 1 represents this relationship.

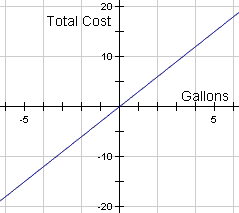Figure 1: Graph of the function t( g ) = 3g which is directly proportional.

Variables can be directly proportional or inversely proportional. The example of gasoline prices is an example of directly proportional. An example of inversely proportional is the time it takes to make a trip as a function of speed. The faster you go, the quicker (less time) you get there. This can be expressed with the function t(s)=100÷s where t( s ) is the time it takes to make the trip, 100 is the distance, and s is the speed of travel. Figure 2 contains a graph of this relationship.

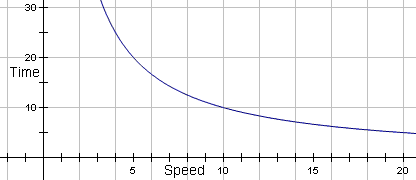Figure 2: Graph of t( s ) = 100 / s which is inversely proportional.

References

1. McAdams, David E.. All Math Words Dictionary, proportional. 2nd Classroom edition 20150108-4799968. pg 146. Life is a Story Problem LLC. January 8, 2015. Buy the book
2. Bettinger, Alvin K. and Englund, John A.. Algebra and Trigonometry. pp 57-58. www.archive.org. International Textbook Company. January 1963. Last Accessed 12/3/2018. http://www.archive.org/stream/algebraandtrigon033520mbp#page/n75/mode/1up/search/proportional. Buy the book

Educator Resources

• Crash - Graphs and NASA Langley. NASA Connect. 2/18/2010. http://www.archive.org/details/NasaConnect-Crash-GraphsAndNasaLangley/index.htm.
• Building Rockets (modeling and ratios). NASA Connect. 2/18/2010. http://www.archive.org/details/NasaConnect-Fof-BuildingRockets/index.htm.
• Building Rockets (modeling and ratios). NASA Connect. 2/18/2010. http://www.archive.org/details/NasaConnect-Fof-BuildingRockets/index.htm.
• Proportionality - Modeling the Future. NASA Connect. 2/18/2010. http://www.archive.org/details/NasaConnect-Proportionality-ModelingTheFuture/index.htm.

Cite this article as:

McAdams, David E. Proportional. 4/21/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/p/proportional.html.

Image Credits

• All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Revision History

12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
12/1/2018: Removed broken links, updated license, implemented new markup. (McAdams, David E.)
8/7/2018: Changed vocabulary links to WORDLINK format. (McAdams, David E.)
9/4/2008: Added 'More Information'. (McAdams, David E.)
6/7/2008: Corrected link errors. (McAdams, David E.)
7/12/2007: Initial version. (McAdams, David E.)