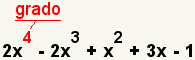Polinomio: Una expresión, generalmente en una variable, con los términos teniendo un coeficiente y una variable elevar a una potencia integral.

Polinomio

3x3 + x2 + 4
Cuadro 1: Un polinomio

3x2 + 2x + 4
Cuadro 2: Polinomio en forma estándar.

2x + 3x2 + 4
Cuadro 3: Polinomio no en forma estándar.

Un polinomio es una expresión con uno o más términos. Cada término tiene un coeficiente y una o más variables cada uno con un exponente integral. La forma estándar de un polinomio es el exponente más alto primero, seguido por el más alto siguiente, y así sucesivamente abajo al término constante. Véase los cuadros 2 y 3.

�ndice del artículo

Términos de polinomios
Grado de un polinomio
Comportamiento del final de polinomios
Raíces de un polinomio
Polinomios especiales
Adición y resta de polinomios
Multiplicación de polinomios
División de polinomios

Términos de polinomios

x^2+2x-4 polinómico. El primer término es x^2. El segundo término es 2x. El tercer término es -4.
Cuadro 4: Términos polinómicos

Cada término de un polinomio es separado de otros términos por la suma o la resta. En el polinomio en el cuadro 4, el primer término es -4. El segundo término es 2x. El tercer término es x2.

Cada término de un polinomio tiene un coeficiente. El coeficiente puede ser cualquier número real. Para el término x2 el coeficiente es 1. La propiedad de multiplicarse por 1 indica ese x2 se implica 1·x2 = x2, así que el 1. Los números reales siguientes pueden ser coeficientes: 1/2, 0.3, π, log210.

Note que un coeficiente puede ser 0. Según la propiedad de multiplicarse por 0 que cualquier cosa mide el tiempo de 0 es 0. En el cuadro uno, el término x no aparece. Esto es porque tiene un término de 0. Este término se puede también escribir 0x. Porque 0x = 0, este término no se escribe normalmente.

Cada término tiene una variable con un exponente del número entero. En el caso del término 2x en el cuadro 2, el exponente de 1 se implica. Esto es porque x1 = x.

El término constante en el cuadro 2 es -4. Si el término constante es 0, no se escribe generalmente.

marca de cheque Cheque de comprensión

Chasque encendido la caja de cheque de la respuesta que usted piensa está correcto.

  1. ¿Es 3x2 - 2x + 1 un polinomio?
    caja de chequeCaja de cheque verde SíSí. Correcto. 3x2 - 2x + 1 es un polinomio. Cada término tiene un coeficiente verdadero y una variable con un exponente del número entero.
    caja de chequeCaja de cheque roja NoNo. Incorrecto. 3x2 - 2x + 1 es un polinomio. Cada término tiene un coeficiente verdadero y una variable con un exponente del número entero.
  2. ¿Es x + 1 un polinomio?
    caja de chequeCaja de cheque verde SíSí. Correcto. x + 1 es un polinomio. Cada término tiene un coeficiente verdadero y una variable con un exponente del número entero.
    caja de chequeCaja de cheque roja NoNo. Incorrecto. x + 1 es un polinomio. Cada término tiene un coeficiente verdadero y una variable con un exponente del número entero.
  3. ¿Es -2x1/2 + 3x - 4 un polinomio?
    caja de chequeCaja de cheque roja SíSí. Incorrecto. En el término -2x1/2, el exponente el 1/2 no es un número entero.
    caja de chequeCaja de cheque verde No. Correcto. En el término -2x1/2, el exponente el 1/2 no es un número entero.
  4. ¿Es 1/2x2 - 8x + 1 un polinomio?
    caja de chequeCaja de cheque verde SíSí. Correcto. 1/2x2 - 8x + 1 es un polinomio. Cada término tiene un coeficiente verdadero y una variable con un exponente del número entero.
    caja de chequeCaja de cheque roja NoNo. Incorrecto. 1/2x2 - 8x + 1 es un polinomio. Cada término tiene un coeficiente verdadero y una variable con un exponente del número entero.
  5. ¿Es -5x2 + 4x un polinomio?
    caja de chequeCaja de cheque verde SíSí. Correcto. -5x2 + 4x es un polinomio. Cada término tiene un coeficiente verdadero y una variable con un exponente del número entero. Observe que el término constante es 0, y así que se omite.
    caja de chequeCaja de cheque roja NoNo. Incorrecto. -5x2 + 4x es un polinomio. Cada término tiene un coeficiente verdadero y una variable con un exponente del número entero. El término constante es 0, y así que se omite.
  6. ¿Es -x2.3 + 1 un polinomio?
    caja de chequeCaja de cheque roja SíSí. Incorrecto. -x2.3 + 1 no es un polinomio. El exponente en el término -x2.3 no es un número entero.
    caja de chequeCaja de cheque verde NoNo. Correcto. -x2.3 + 1 no es un polinomio. El exponente en el término -x2.3 no es un número entero.
  7. ¿Es 3 un polinomio?
    caja de chequeCaja de cheque verde SíSí. Correcto. Un constante se puede considerar un polinomio degenerado. Este polinomio se puede escribir 3x0, desde x0 = 1.
    caja de chequeCaja de cheque roja NoNo. Incorrecto. Un constante se puede considerar un polinomio degenerado. Este polinomio se puede escribir 3x0, desde x0 = 1.

Grado de un polinomio

El polinómico 2x^4-2x^3+x^2+3x-1 es el grado 4.
Cuadro 5 - Polinomio del grado 4

El grado de un solo polinomio variable es el exponente más alto. En el cuadro 5, el exponente más alto es 4, así que el grado del polinomio es 4.

marca de cheque Cheque de comprensión

Chasque encendido la caja de cheque de la respuesta que usted piensa está correcto.
  1. ¿Cuál es el grado del polinómico 3x2 - 2x + 1?
    caja de chequeCaja de cheque roja 00: Incorrecto. Hay un término con un exponente de 0, pero el exponente más alto es 2, así que el grado del polinomio es 2.
    caja de chequeCaja de cheque roja 11: Incorrecto. Hay un término con un exponente de 1, pero el exponente más alto es 2, así que el grado del polinomio es 2.
    caja de chequeCaja de cheque verde 22: Correcto. El exponente más alto es 2, así que el grado del polinomio es 2.
    caja de chequeCaja de cheque roja 33: Incorrecto. No hay término con un exponente 3. El exponente más alto es 2, así que el grado del polinomio es 2.
    caja de chequeCaja de cheque roja 44: Incorrecto. No hay término con un exponente 4. El exponente más alto es 2, así que el grado del polinomio es 2.
    caja de chequeCaja de cheque roja 55: Incorrecto. No hay término con un exponente 5. El exponente más alto es 2, así que el grado del polinomio es 2.
  2. ¿Cuál es el grado del polinómico -3x4 + 2x3 - 2x + 1?
    caja de chequeCaja de cheque roja 00: Incorrecto. Hay un término con un exponente 0, pero el exponente más alto es 4, así que el grado del polinomio es 4.
    caja de chequeCaja de cheque roja 11: Incorrecto. Hay un término con un exponente 1, pero el exponente más alto es 4, así que el grado del polinomio es 4.
    caja de chequeCaja de cheque roja 22: Incorrecto. No hay término con un exponente 2. El exponente más alto es 4, así que el grado del polinomio es 4.
    caja de chequeCaja de cheque roja 33: Incorrecto. Hay un término con un exponente 3, pero el exponente más alto es 4, así que el grado del polinomio es 4.
    caja de chequeCaja de cheque verde 44: Correcto. El exponente más alto es 4, así que el grado del polinomio es 4.
    caja de chequeCaja de cheque roja 55: Incorrecto. No hay término con un exponente 5. El exponente más alto es 4, así que el grado del polinomio es 4.
  3. ¿Cuál es el grado de los 6 polinómicos?
    caja de chequeCaja de cheque verde 00: Correcto. Un constante se puede considerar un polinomio del grado 0.
    caja de chequeCaja de cheque roja 11: Incorrecto. Un constante se puede considerar un polinomio del grado 0.
    caja de chequeCaja de cheque roja 22: Incorrecto. Un constante se puede considerar un polinomio del grado 0.
    caja de chequeCaja de cheque roja 33: Incorrecto. Un constante se puede considerar un polinomio del grado 0.
    caja de chequeCaja de cheque roja 44: Incorrecto. Un constante se puede considerar un polinomio del grado 0.
    caja de chequeCaja de cheque roja 55: Incorrecto. Un constante se puede considerar un polinomio del grado 0.

Grado de polinomios multivariantes

El grado de un polinomio multivariante es la suma más alta de los exponentes en las variables. Por ejemplo, el polinómico x2y + 3x2y3 tiene un grado de 5: (2 + 3 = 5).

Comportamiento del final de polinomios

espacio vacíoTérmino positivoTérmino negativo
Grado parGráfico de x^2+3x-1 con ambos finales del polinomio que señala hacia arriba.Gráfico - de x^2+3x+1 con ambos finales del polinomio que señala hacia abajo.
Grado imparGráfico de 2x^3-x^2-5x-1 con el extremo izquierdo que señala abajo y el extremo correcto que destaca.Gráfico de -2x^3-x^2+5x-1 con el final izquierdo del polinomio que señala hacia arriba y el extremo correcto que señala hacia abajo.
Cuadro 1: Comportamiento del final de polinomios.

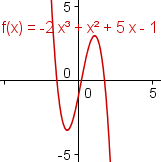
Como la discusión de un polinomio se mueve hacia positivo o el infinito negativo, el valor del polinomio también se mueve hacia infinito positivo o negativo. Esto se llama el comportamiento del final del polinomio.

Para los polinomios con grado par, ambos extremos del punto polinómico en la misma dirección. Para los polinomios con grado impar, los extremos del punto polinómico en diversas direcciones. Los polinomios con un término positivo del grado más alto van para arriba a la derecha. Los polinomios con un término negativo del grado más alto van abajo a la derecha.

Lo sentimos, pero la GeoGebra Applet no se pudo iniciar. Por favor, asegúrese de que Java 1.4.2 (o posterior) está instalado y activo en su navegador ( Haga clic aquí para instalar Java ahora )
El manipulante 1: Comportamiento polinómico del final. Creado con GeoGebra.

Chasque encendido los puntos azules en los resbaladores en el manipulante 1 para cambiar los valores. Si la signo de término mas grande es positiva, el derecho del polinomio va hacia infinito. Si la signo de término mas grande es negativa, el derecho del polinomio va hacia infinito negativo. Si el grado es par, el lado izquierdo del polinomio va hacia el mismo valor que el derecho. Si el grado del polinomio es impar, el lado izquierdo del polinomio va hacia el valor opuesto del derecho.

Raíces de un polinomio

Las raíces de un polinomio son los valores que la variable de un polinomio puede tomar cuando el polinomio se fija igual a cero. Una raíz de un polinomio se puede también llamar un cero de un polinomio. Por ejemplo, tome el binomial x - 3. La determinación del binomio a cero da x - 3 = 0. El solucionar para x da x = 3. Tan 3 es un cero del binomial x-3. Uno puede también decir que 3 es una raíz del x binomial -3. Para más información sobre encontrar raíces de polinomios, vea descomponer en factores polinomios.

Polinomios especiales

Un polinomio del grado 2 se llama una ecuación cuadrática. Un polinomio del grado 3 se llama un cúbico. Un polinomio con 2 términos se llama un binomio.

Suma y resta de polinomios

Lo sentimos, pero la GeoGebra Applet no se pudo iniciar. Por favor, asegúrese de que Java 1.4.2 (o posterior) está instalado y activo en su navegador ( Haga clic aquí para instalar Java ahora )
El manipulante 2: Sumar de polinomios. Creado con GeoGebra.

Cuando se agrega junto el suma de dos polinomios, términos semejantes. La manera más fácil de hacer esto es poner los polinomios en la forma estándar, una debajo de la otra. La suma de polinomios es asociativa: P(x)+ [Q(x)+R(x)] = [P(x)+Q(x)] +R(x)]. La suma de polinomios es comutativa: P(x)+Q(x) = Q(x)+P(x).

Chasque encendido los puntos rojos y verdes en el manipulante 1 y arrástrelos para cambiar la figura.

Descubrimiento

  1. ¿Qué forma hace h(x) hicieron si a1 = -a2?
    Tecleo para la indirecta.
  2. ¿Si f(x) se abre hacia arriba (a1 > 0) y g(x) se abre hacia abajo (a2 < 0), en la cual la dirección h(x) se abrieron?
    Tecleo para la indirecta.

Ejemplos

PasoEcuacionesDescripción
1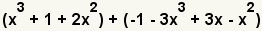(x^3+1+2x^2)+ (- 1-3x^3+3x-x^2)Éstos son los polinomios a agregar.
2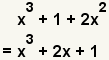x^3+1+2x^2=x^3+2x^2+1Ponga el primer polinomio en forma estándar, del término del grado más alto al más bajo.
3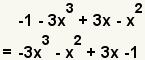-1-3x^3+3x-x^2=-3x^3-x^2+3x-1Ponga el segundo polinomio en forma estándar, del término del grado más alto al más bajo.
4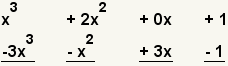(x^3+2x^2+1)+ (- 3x^3-x^2+3x-1) =-2x^3+x^2+3x+0Alinéese los polinomios, uno debajo del otro. Puesto que el primer polinomio no tiene un término de “x�, complete 0x.
5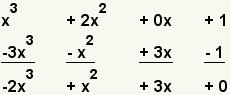(x^3+1+2x^2)+ (- 1-3x^3+3x-x^2)=-2x^3+x^2+3x+0 Agregue los términos verticalmente.
6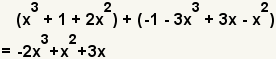(x^3+1+2x^2)+ (- 1-3x^3+3x-x^2)=-2x^3+x^2+3xÉste es el resultado.
Ejemplo 1

La resta de polinomios es como la suma de polinomios. En vez del suma términos semejantes, uno resta términos semejantes. La resta de polinomios es asociativa: P(x) - [Q(x) - R(x)] = [P(x) - Q(x)] - R(x)]. La resta de polinomios no es comutativa: P(x) - Q(x) ≠ Q(x) - P(x).

PasoEcuacionesDescripción
1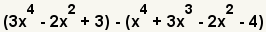Éstos son los polinomios a restar.
2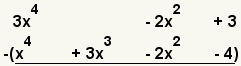Ponga los polinomios en la forma estándar, una debajo de la otra.
3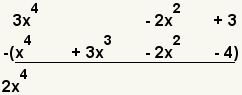Reste los términos del grado más alto. 3x4 - x4 = 2x4.
4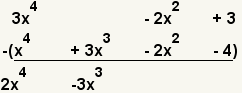Reste los términos siguientes del grado más alto. 0x3 - 3x3 = -3x3.
5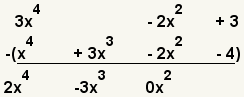Repita el proceso con los términos siguientes. -2x2 - -2x2 = 0x2.
6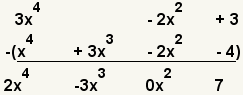Repita el proceso con los términos siguientes. 3 - -4 = 7.
7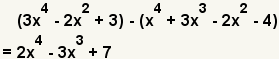Éste es el resultado.
Ejemplo 2

Multiplicación de polinomios

Para multiplicar polinomios, multiplique cada uno de los términos del primer polinomio por cada uno de los términos del segundo polinomio. Entonces agregue términos semejantes. La multiplicación de polinomios es asociativa: P(x)·[Q(x)·R(x)] = [P(x)·Q(x)]·R(x)]. La multiplicación de polinomios es comutativa: P(x)·Q(x) = Q(x)·P(x).

Ejemplos

PasoEcuacionesDescripción
1(x^3+2x^2+1)* (3x^3-x^2+3x-1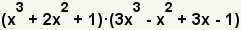)Éstos son los polinomios a multiplicarse.
2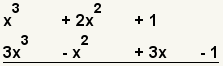(x^3+2x^2+1)* (3x^3-x^2+3x-1)Alinee los polinomios uno debajo del otro.
3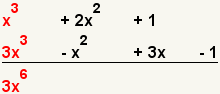(x^3+2x^2+1)* (3x^3-x^2+3x-1) =3x^6…Multiplique los primeros términos de los polinomios.
4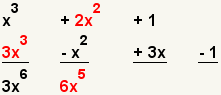(x^3+2x^2+1)* (3x^3-x^2+3x-1) =3x^6-2x^4…Multiplique el segundo término del primer polinomio con el primer término del segundo polinomio.
5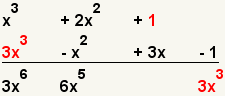(x^3+2x^2+1)* (3x^3-x^2+3x-1) =3x^6-2x^4…Multiplique el tercer término del primer polinomio con el primer término del segundo polinomio.
6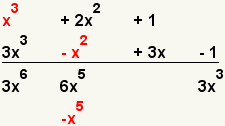(x^3+2x^2+1)* (x^3+2x^2=1)Multiplique el primer término del primer polinomio con el segundo término del segundo polinomio.
7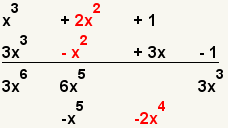(x^3+2x^2+1)* (x^3+2x^2=1)Multiplique el segundo término del primer polinomio con el segundo término del segundo polinomio.
8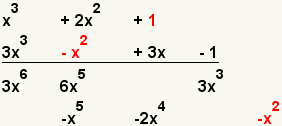(x^3+2x^2+1)* (x^3+2x^2=1)Multiplique el tercer término del primer polinomio con el segundo término del segundo polinomio.
9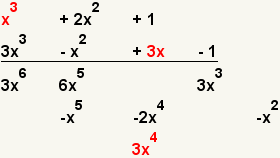(x^3+2x^2+1)* (x^3+2x^2=1)Multiplique el primer término del primer polinomio con el tercer término del segundo polinomio.
10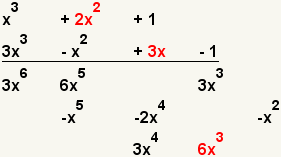(x^3+2x^2+1)* (x^3+2x^2=1)Multiplique el segundo término del primer polinomio con el tercer término del segundo polinomio.
11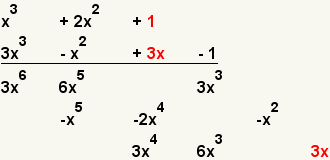(x^3+2x^2+1)* (x^3+2x^2=1)Multiplique el tercer término del primer polinomio con el tercer término del segundo polinomio.
12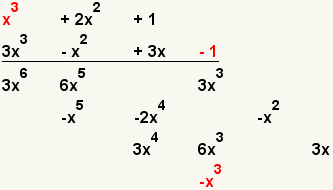(x^3+2x^2+1)* (x^3+2x^2=1)Multiplique el primer término del primer polinomio con adelante el término del segundo polinomio.
13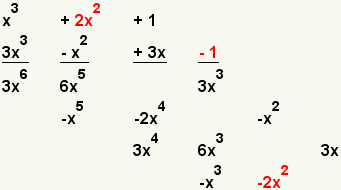(x^3+2x^2+1)* (x^3+2x^2=1)Multiplique el segundo término del primer polinomio con adelante el término del segundo polinomio.
14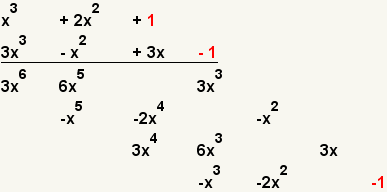(x^3+2x^2+1)* (x^3+2x^2=1)Multiplique el tercer término del primer polinomio con adelante el término del segundo polinomio.
15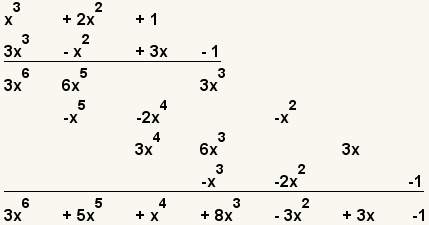(x^3+2x^2+1)* (x^3+2x^2=1)Agregue todos los términos de los similares.
16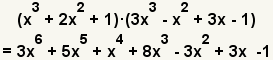(x^3+2x^2+1)* (x^3+2x^2=1)=3x^6+5x^5+x^4+8x^3-3x^2+3x-1Éste es el resultado.
Ejemplo 3

División de polinomios

La división de polinomios es mucho como la división larga. En vez de ocuparse de los dígitos, uno se ocupa de los términos del polinomio. La división de polinomios es asociativa: P(x)÷ [Q(x)÷R(x)] = [P(x)÷R(x)]÷Q(x). La división de polinomios no es comutativa: P(x)÷Q(x) ≠ Q(x)÷P(x).

Ejemplos

PasoEcuacionesDescripción
1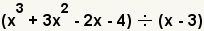(x^3+3x^2-2x-4)/(x-3)En este ejemplo, dividiremos el polinomio
x3 + 3x2 - 2x - 4 por x - 3.
2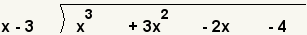x-3 entra a x^3+3x^2-2x-4Arregle los polinomios como la división larga con el divisor a la izquierda y el dividendo a la derecha.
3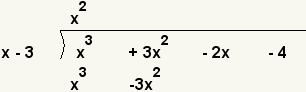(x^3+2x^2+1)* (3x^3-x^2+3x-1)¿Qué valor por x iguala x3? x · x2 = x3. Ponga tan x2 en la tapa y el producto de x2 y x - 3 en la parte inferior. x2·(x - 3) = x3 - 3x2.
4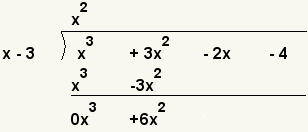(x^3+2x^2+1)* (3x^3-x^2+3x-1)Reste x3 - 3x2 del dividendo. (x3 + 3x2) - (x3 - 3x2) = 0x3 + 6x2.
5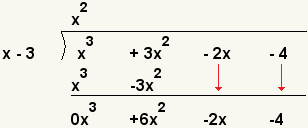(x^3+2x^2+1)* (3x^3-x^2+3x-1)Derribe el resto de los términos.
6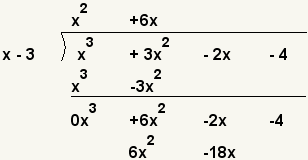(x^3+2x^2+1)* (3x^3-x^2+3x-1)¿Qué valor por x iguala 6x2? x · 6x = 6x2. Ponga tan 6x en la tapa y el producto de 6x y x - 3 en la parte inferior. 6x·(x - 3) = 6x2 - 18x.
7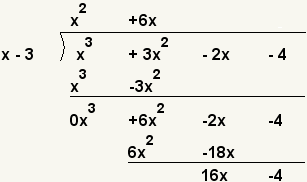(x^3+2x^2+1)* (3x^3-x^2+3x-1)Reste 6x2 - 18x de la diferencia pasada. (6x2 - 2x) - (6x2 - 18x) = 0x2 + 16x. Derribe el último período.
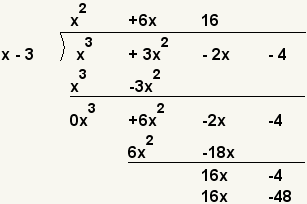8(x^3+2x^2+1)* (3x^3-x^2+3x-1)¿Qué valor por x iguala 16x? x · 16 = 16x. Ponga tan 16 en la tapa y el producto de 16 y x - 3 en la parte inferior. 16·(x - 3) = 16x - 48.
9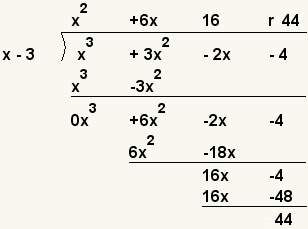(x^3+2x^2+1)* (3x^3-x^2+3x-1)Reste 6x - 48 de la diferencia pasada. (16x - 4) - (16x - 48) = 44.
10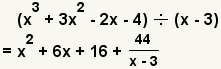(x^3+2x^2+1)* (3x^3-x^2+3x-1)Puesto que x - 3 no pueden entrar uniformemente 44, 44 es el resto.
Ejemplo 4

Regla de Ruffini

Vea la Regla de Ruffini.

Descomponer en factores polinomios

Vea descomponer en factores polinomios.

Más información

  • McAdams, David. Grado de una ecuación. AllMathWords.org. Life is a Story Problem.org. 2009-04-03. https://www.allmathwords.org/article.aspx?lang=es&id=Degree%20of%20an%20Equation.
  • McAdams, David. Término. AllMathWords.org. Life is a Story Problem.org. 2009-04-03. https://www.allmathwords.org/article.aspx?lang=es&id=Term.
  • Cuervo, Leoncio Santos. Polinomios. descartes.cnice.mec.es. Ministerio de Educación, Política Social y Deporte. 2009-05-04. http://descartes.cnice.mec.es/materiales_didacticos/Polinomios/polinomios1.htm.

Citar este artículo como:
Polinomio. 2009-04-03. Enciclopedia de Todas las Palabras de la Matemáticas. Life is a Story Problem.org. https://www.allmathwords.org/es/p/polynomial.html.

Traducciones

créditos de imagen

  • Todas las imágenes y manipulatives están por David McAdams a menos que estén indicadas de otra manera. Todas las imágenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.

La historia de revisión


2009-04-03: Traducido automáticamente por BabelFish. (babelfish.yahoo.com.)
2009-02-10: Reescribió la sección en comportamiento del final (McAdams, David.)
2009-02-06: Secciones agregadas en la adición, la multiplicación y la división de polinomios (McAdams, David.)
2009-01-29: Sección agregada en raíces de polinomios (McAdams, David.)
2009-01-20: Referencia agregada a descomponer en factores polinomios (McAdams, David.)
2008-12-17: '' Comportamiento agregado del final de polinomios '' (McAdams, David.)
2008-05-01: Info agregado para los polinomios variables múltiples y la forma estándar (McAdams, David.)
2008-04-04: Versión inicial (McAdams, David.)

Enciclopedia de Todas las Palabras de la Matemáticas es un servicio de Life is a Story Problem.org.
Los derechos reservados ©2005-2009 de Life is a Story Problem.org. Todos los derechos reservados.
Creative Commons License Este trabajo se autoriza debajo de una Creative Commons Attribution-Noncommercial-Share Alike 3.0 License