Complement (Set)
Pronunciation: /ˈkɒm.plə.mənt/ ExplainUniversal Set
|
The concept of complement starts with a universal set. A universal set is a set that contains all elements one wishes to include. If one is dealing with numbers, the universal set might be all real numbers, or all integers. Other possibilities for the universal set is all animals, or all students in a class. A universal set is usually represented by a box. |
Complement of a Set
|
The complement of a set is all elements of the universal set that are not elements of the set. In figure 2, the universal set is S. The set A is represented by the blue interior of the circle. The complement of A is the blue part of S that is not inside the circle A. To write a complement, write A\S or A'. To talk about a complement say, "The complement of A in S," or "The complement of A." ExamplesLet the universal set S be the set of all integers. Let A be the set of all even integers. The complement of A in S is all integers which are not even numbers. This means the complement of A is all odd numbers. This can be written mathematically as: S = { x | x ∈ Integers }
A = { x | x = 2k, k ∈ S }
B = A / S
B = A'
B = { x | x = 2k + 1, k ∈ S }
Let S be the set of all students in a classroom. Let A be the set of all the female students in the classroom. Let B be the set of all male students in the classroom. Since each student is either male or female, A = B'. |
Non-Complementary Sets
|
Two sets are not complementary if the two sets together do not include the entire universal set. In figure 3, set S is the universal set. There are parts of set S that are not in either set C or set D. So D is not the complement of C. Stated mathematically: C ∪ D ≠ S ⇒ C / S ≠ D
E ∩ F ≠ ∅ ⇒ E / S ≠ F
ExamplesLet S be the set of all animals. Let C be the set of all cats. Let D be the set of all dogs. Since there are animals that are neither dogs nor cats, C is not the complement of D in S. Let S be the set of all fruit. Let C be the set of all apples. Let D be the set of all oranges. Since there are fruit that are neither apples nor oranges, C is not the complement of D. Sets are also not complementary if they overlap; if they contain some of the same members: ( E ∩ F ≠ ∅ ). In figure 4, sets E and F contains some common members. Stated mathematically:
E ∩ F ≠ ∅ ⇒ E / S ≠ F
ExampleLet S be the set of all students in a school. Let E be all students with brown hair. Let F be all male students. Since some male students also have brown hair, the sets overlap. So F is not the complement of E. |
Formal Definition
|
Given a set S and a subset A of S, the complement of A is a set of all members of S that are not members of A. If set B is the complement of A, write B = A'. The definition of the complement of A in S is written in set notation as A \ S = {x ∈ B | x ∈ S and x ∉ A }. |
Complement Theorems
A \ (B ∩ C) = (A \ B) ∪ (A \ C)
The complement of an intersection of sets is equal to the union of the complement of each set.
| Statement | Justification | |
|---|---|---|
| A \ (B ∩ C) = | {x | x ∈ A and x ∉ (B ∩ C)} | Translate to set notation. |
| {x | x ∈ A and (x ∉ B or x ∉ C)} | Intersection of sets | |
| {x | ( x ∈ A and x ∉ B ) or ( x ∈ A and x ∉ C)} | Distributive property | |
| (A \ B) ∪ (A \ C) | Translate back to algebraic notation | |
| Table 1: Complement of the intersection of two sets. | ||
A \ (B ∪ C) = (A \ B) ∩ (A \ C)
The complement of an union of sets is equal to the intersection of the complement of each set.
| Statement | Justification | |
|---|---|---|
| A \ (B ∪ C) = | {x | x ∈ A and x ∉ (B ∪ C)} | Translate to set notation. |
| {x | x ∈ A and (x ∉ B or x ∉ C)} | Definition of union of sets | |
| {x | (x ∈ A and x ∉ B) or (x ∈ A and x ∉ C)} | Distributive property | |
| (A \ B) ∩ (A \ C) | Transform back to algebraic notation | |
| Table 2: Complement of the union of two sets. | ||
De Morgan's Laws[4]
De Morgan's Law for the intersection of sets - (A ∩ B)' = A' ∪ B'
The complement of an intersection of sets is equal to the union of the complements of the sets.
| Proof of De Morgan's Law for the Intersection of Sets | |||
| Illustration | Statement | Justification | |
|---|---|---|---|
| Prove that (A ∩ B)' = A' ∪ B' by showing that (A ∩ B)' and A' ∪ B' are subsets of each other. | Claim | ||
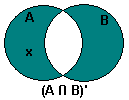 |
Let x ∈ (A ∩ B)' | Assumption | |
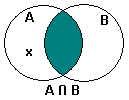 |
Then x ∉ (A ∩ B) | Definition of the complement of a set | |
 |
Hence x ∉ A or x ∉ B. | Definition of the Intersection of Sets. | |
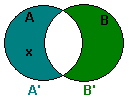 |
So x ∈ A' or x ∈ B' | Definition of the complement of a set. | |
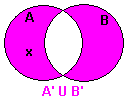 |
So x ∈ (A' ∪ B') | Definition of the union of a set. | |
| Table 3: De Morgan's Law for the intersection of sets. | |||
De Morgan's Law for the union of sets - (A ∪ B)' = A' ∩ B'
The complement of a union of sets is equal to the intersection of the complements of the sets.
References
- McAdams, David E.. All Math Words Dictionary, complement. 2nd Classroom edition 20150108-4799968. pg 38. Life is a Story Problem LLC. January 8, 2015. Buy the book
- complement. merriam-webster.com. Encyclopedia Britannica. Merriam-Webster. Last Accessed 6/25/2018. http://www.merriam-webster.com/dictionary/complement. Buy the book
- Couturat, Louis. The Algebra of Logic. Sect 0.25 pg 26. Translated by Lydia Gillingham Robinson, B. A.. Open Court Publishing. 1914. Last Accessed 6/25/2018. http://www.gutenberg.org/files/10836/10836-pdf.pdf. Buy the book
- Goldrei, D.C.. Classic Set Theory: For Guided Independent Study. pg 4. Chapman & Hall Mathematics. July 1 1996. Last Accessed 6/25/2018. Buy the book
- Gilbert, Jimmie; and Gilbert Linda. Elements of Modern Algebra. 6th edition. pp 5-6,9. Thomson, Brooks/Cole, 2005.. Last Accessed 6/25/2018. Buy the book
More Information
- McAdams, David E.. Set. allmathwords.org. All Math Words Encyclopedia. Life is a Story Problem LLC. 6/27/2018. https://www.allmathwords.org/en/s/set.html.
Cite this article as:
McAdams, David E. Complement (Set). 4/16/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/c/complementset.html.Image Credits
- All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Revision History
4/16/2019: Updated equations and expressions to new format. (McAdams, David E.)3/6/2019: Minor formatting changes. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
6/25/2018: Removed broken links, updated license, implemented new markup, updated GeoGebra apps. (McAdams, David E.)
1/4/2010: Added "References". (McAdams, David E.)
7/8/2008: Expanded and simplified first paragraph. (McAdams, David E.)
3/31/2008: Initial version. (McAdams, David E.)
- Navigation
- Home
- Contents
-
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z - Teacher Aids
- Classroom Demos
- How To
- LIASP
- LIASP Home
- Conditions of Use
- Privacy Policy
- Donate to LIASP
- Help build this site
- About LIASP
- Contact LIASP
All Math Words Encyclopedia is a service of
Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License


