Set

Pronunciation: /sɛt/ Explain

A set is a collection of objects about which membership can be established. A set can have a finite number of members, or an infinite number of members. Examples of sets include the set of integers, the set of positive numbers, and the set of even numbers.

The study of sets is called set theory. Set theory forms one of the bases of modern mathematics.

Sets are conventionally referred to by a capital letter. When printing text including a letter for a set, the letter is italicized: "Let set Z be the set of all integers." For more on set notation, see Set Notation.

Membership in sets

Figure 1: p ∈ A, q ∉ A

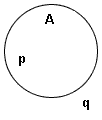
An object that is a member of a set is called an element of the set. If object p is an element of set A, one writes p ∈ A and says "p is an element of A". If object q is not an element of set A, one writes q ∉ A.

Uniqueness of sets

A set is uniquely determined by its members. This means that there is only one set with that set of members. For example, there is only one set of all integers. If two sets contain all integers, then they are the same set.

Special sets

An important set is called the empty set. The empty set is unique; there is only one empty set. Another important set is the universal set. The universal set contains all elements being considered. If one is talking about complex numbers, the universal set can be considered to be the set of all complex numbers.

Relations between sets

Figure 2: A ⊂ B, B ⊃ A

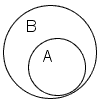
Subset If all the elements of set A are also in set B, then set A is a subset of set B. One writes A⊂B and says "A is a subset of B". If set A is a subset of set B and may be equal to B, one writes A ⊆ B. If set B is not a subset of set C, one writes B ⊄ C. Superset The inverse of subset is superset. If set A is a subset of set B, then set B is a superset of set A. One writes B ⊃ A. If set A is a proper subset of set B, then set B is a proper superset of set A. one writes B ⊇ A.

Equality

Two sets are equal if they contain exactly the same members. This is stated formally as: Given sets A and B, A = B if and only if A ⊂ B and B ⊂ A.

Operations on Sets

Power Set

A power set of a set is the set of all subsets of a set. For example, the power set of set A = {1 ,3, 6} is ℘(A) = {∅, {1}, {3}, {6}, {1, 3}, {1, 6}, {3, 6}, {1, 3, 6}}.

Union

Figure 3: A ∪ B

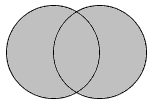
A union of two sets is a set that contains all the elements in either set. One writes the union of set A and B as A ∪ B. For example, if set A and B are defined as A = { 1, 3, 5, 7 } and B = { 1, 2, 3, 4 }, then A ∪ B = { 1, 2, 3, 4, 5, 7 }. Some of the properties of the union of sets are: A ∪ ∅ = A - The union of any set A and the empty set is equal to the set A. If B ⊂ A then A ∪ B = A. The union of any set A and any of its subset is set A.

Intersection

Figure 4: A ∩ B

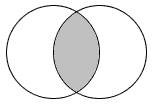
An intersection of two sets is a set containing all the elements that are in both of the sets. One writes the intersection of set A and set B as A ∩ B. For example, if set A and B are defined as A = { 1, 3, 5, 7 } and B = { 1, 2, 3, 4 }, then A ∩ B = { 1, 3 }. Some of the properties of intersection of sets are: A ∩ ∅ = ∅ - The intersection of a set and the empty set is the empty set. If B ⊆ A then A ∩ B = B - The intersection of a set A and its subset B is the subset B.

Complement

Figure 5: Complement of A.

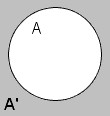
The complement of a set is all elements of the universal set that are not members of that set. For example, if the universal set is the set of all integers (ℤ), and set A is the set of all even integers, then the complement of set A is the set of all odd integers. If set B is the complement of set A one writes B = A'. Some of the properties of complements are: Let B = A'. Then B' = A. The complement of the complement of set A is set A. If U be the universal set. U' = ∅ - The complement of the universal set is the empty set. If U be the universal set. ∅' = U - The complement of the empty set is the universal set. ( A ∩ B )' = A' ∪ B' - The complement of the intersection of two sets is the union of the complements. (de Morgan's Theorem) ( A ∪ B )' = A' ∩ B' - The complement of the union of two sets is the intersection of the complements. (de Morgan's Theorem)

Cartesian Product

The Cartesian product of two sets is a set of ordered pairs that contains one member of the first set and one member of the second set. Every combination of members of the two sets is represented. The Cartesian product of sets A and B is written A × B. The Cartesian product of the set A with itself is written A². The Cartesian product of the sets A = { a, b } and B = { c, d, e } is { (a,c), (a,d), (a, e), (b, c), (b, d), (b, e)}.

Properties of Sets

Some properties of sets are:

• Cardinality - The cardinality of a set is the size of a set. If a set has a finite number of members, then the cardinality of the set is the number of members. If a set has an infinite number of members, then the cardinality of the set is either countably infinite, or uncountably infinite. For more information on cardinality, see Cardinality.
• Order - A set is ordered if, for any two distinct members of a set a and b, either a < b or b < a. A set is ordered if one can always tell if one element comes before or after another element.
• Continuity - An ordered set is continuous if there are no "gaps" or "holes" in it. One of the properties of a continuous set is that between any two members of a set, there is at least one other member of the set. A set that is not continuous is called discontinuous.
• Countable - A set is countable if it is a finite set, or if the set has a one to one correspondence with the set of natural numbers. If a set is not countable, then it is uncountable. The word denumerable means the same thing as countable. The word nondenumerable means the same thing as uncountable.
• Discrete - A set is discrete if the members of the set are isolated. A set is discrete if no subset forms a continuum.
• Finite - A set is finite if it has a finite number of members. A set is finite if, when enumerating the elements of the set, a last element can be found. A set that is not finite is infinite.
• Bounded - A set is bounded if it has a upper bound and a lower bound. An upper bound is a value that is greater than any member of the set. A lower bound is a value that is less than any member of the set. A set that is not bounded is called unbounded.
• Least upper bound - The least upper bound of an ordered set is least value that is greater than or equal to any member of a set. A least upper bound may or may not be a member of the set. Example: 5 is a least upper bound of the sets { x | x < 5 } and { y | -1 ≤ y ≤ 5}. A least upper bound is also called a supremum.
• Greatest lower bound - The greatest lower bound of an ordered set is greatest value that is less than or equal to any member of a set. A greatest lower bound may or may not be a member of the set. Example: 2 is a greatest lower bound of the sets { x | x > 2} and { y | 2 ≤ y ≤ 7}. A greatest lower bound is also called an infimum.

Standard Sets

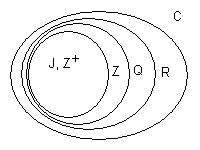
Figure 1: Standard sets

A number of standard sets are denoted by convention. Notation Description Z, ℤ The set of all integers J, Z+, ℤ+ The set of all positive integers. Q, ℚ The set of all rational numbers. R, ℝ The set of all real numbers. C, ℂ The set of all complex numbers.

Types of Sets

Some commonly used types of sets are:

• Binary - A binary set is a set with exactly two members. Boolean algebra is an algebra on a particular binary set.
• Ordered pair - An ordered pair is a set containing two members where the order of the members is important. ( x, y ) is different from ( y, x).
• Ordered triple - An ordered triple is a set containing three members where the order of the members is important. ( x, y, z) is different from ( y, x, z ), ( z, x, y ) and ( z, y, x ).

References

1. McAdams, David E.. All Math Words Dictionary, set. 2nd Classroom edition 20150108-4799968. pg 163. Life is a Story Problem LLC. January 8, 2015. Buy the book

More Information

• J J O'Connor and E F Robertson. A history of set theory. School of Mathematics and Statistics, University of St Andrews, Scotland. 1/11/2010. http://www-groups.dcs.st-and.ac.uk/~history/HistTopics/Beginnings_of_set_theory.html.

Cite this article as:

McAdams, David E. Set. 5/4/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/s/set.html.

Image Credits

• All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Revision History

5/4/2019: Changed equations and expressions to new format. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
12/6/2018: Removed broken links, updated license, implemented new markup. (McAdams, David E.)
8/7/2018: Changed vocabulary links to WORDLINK format. (McAdams, David E.)
9/30/2010: Expanded article to include more properties of sets. (McAdams, David E.)
12/15/2009: Rewrote article. (McAdams, David E.)
5/4/2009: Added double struck symbology for standard sets. (McAdams, David E.)
3/28/2008: Added standard sets. (McAdams, David E.)
7/12/2007: Initial version. (McAdams, David E.)