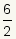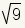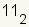Number

Pronunciation: /ˈnʌm.bər/ Explain

A number is a representation of a quantity. A quantity answers the questions, "How many?" and "How much?"

Figure 1: 3 apples

In figure 1 there are three apples. We can use different characters to represent the quantity:

3
three
3.0

4 - 1


Table 1: Representations of the quantity 3

How many ways can you think of to represent 3?

Related Words

Numeric

Numerical

Numerically

Quantity

Digits and Place Value

The digits of the number 374 is 3 in the hundred's place, 7 in the ten's place and 4 in the ones place.

Figure 2: Digits and place value

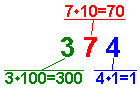
Each digit of a number has a place value. The position of the digit in the number tells the place value. For the decimal numbers, the place values are multiple of 10. Figure 2 shows a number without a decimal point. This means that the digit on the extreme right of the number has a place value of 1. The total value of the digit is 4 · 1 = 4. The digit following to the left is 7'. The place value of this digit is 1 · 10 = 10. The total value of the digit is 10 · 7 = 70. The digit to the left has a place value of 10 · 10 = 100. The total value of the digit is 3 · 100 = 300. The value of the number in figure 2 is 300 + 70 + 4.

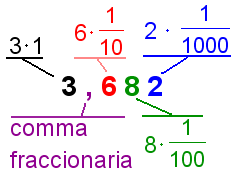
The digits of the number 3.682, 6 is in the tenth's place, 8 is in the hundredth's place, and 2 is in the thousandth's place

Figure 3: Digits and place value to the right of the decimal point.

In figure 3, number 3.682 has a decimal point. The digit to the left of the decimal has a place value of 1. The digit to the right of the decimal has a place value of 1/10. Each digit further to the right of the decimal point has a place value of 1/10 of the previous digit. So the 6 has a total value of 6 · 1/10 = 6/10. The following digits have values of 8 · 1/100 = 8/100 and 2 · 1/1000. The value of the integral number is 3 + 6/10 + 8/100 + 2/1000.

Parts of a Number

Parts of a decimal number: sign, whole part, decimal, part less than one

Figure 4: Parts of a number.

A number can consist of digits, a decimal point, a positive or negative sign (+ or -), and a comma separator.

Other Representations of Quantity

Seven hash marks. Each has mark is a vertical line segment.

Figure 5: Seven hash marks

Quantities have been represented in many ways. One way that was in early use was hash marks. Each line counts as one. In the example in figure 5, there are seven lines. So the quantity represented is seven.

Figure 6: A notched bone, which may have been used as a musical instrument or a counting device, was found in an Early Bronze Age (2900 B.C.) grave at Kenan Tepe, Turkey.
Photographer: Bradley J. Parker

Sticks and bones have been found at archaeological sites with notches cut in them to make hash marks. Hash marks have several problems. Zero can not be represented by hash marks. Also, very large numbers are awkward to represent with has marks. Only natural numbers can be represented by hash marks.

Brass counters and Counting boards were used to calculate numbers before calculators were invented. Figure 7 shows brass counters used at Jamestown.

Brass counter markers excavated from Jamestown

Figure 7: Brass counters excavated from Jamestown.

Numbers have evolved as the best way to represent quantities. They can represent positive numbers, zero, and negative numbers. They can represent very large and very small numbers. They can also represent non-whole quantities such as 1.5. The only thing numbers can not represent exactly is irrational quantities. The digits in irrational values go on forever without repeating, so an irrational value can not be represented with a finite number of digits. Other representations such as π and √2 are used to represent irrational numbers exactly.

Types of Numbers

ℂ: Complex number
ℝ: Real number
Double struck I

: Imaginary number
ℚ: Rational number
ℤ: Integer
ℕ: Natural number (counting numbers)

Figure 8: Number Types

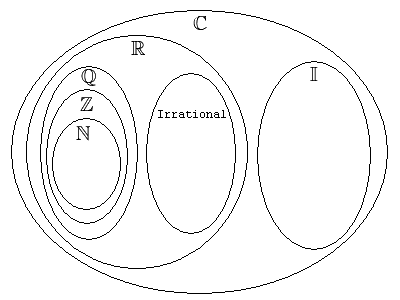
Mathematicians have divided numbers into groups according to their properties. Figure 8 is a Venn diagram of number types. The group of complex numbers contains all other groups of numbers. All numbers are complex numbers. Table 2 gives the properties of the types of numbers.

Types of Numbers
Type	Symbol	Description	Examples
Complex Number	ℂ	A complex number is a number with a real part and an imaginary part. The real part is any real number. The imaginary part is a real number multiplied by `i`. `i` represents √-1. Since the coefficient of the imaginary part can be 0, all real numbers are also complex numbers.	3+2i -2.7 + 4i e^3.7i
Real Number	ℝ	A real number is a number that can be found on the real number line. All real numbers are also complex numbers. Stated mathematically: ℝ ⊂ ℂ.	4 3.74 e^2.0 √5 π 3.5193
Imaginary Number		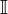An imaginary number is a complex number with no real part. All imaginary numbers are also complex numbers.	4i 3.74i e^3πi/2 √-3
Rational Number	ℚ	A rational number is a real number that can be expressed as the ratio of two integers. A number with a repeating decimal is a rational number, as all repeating decimals can be expressed as a ratio of integers. All rational numbers are also real numbers. Stated mathematically: ℚ ⊂ ℝ.	4 Why? 3/7 √9 Why? 3.5193 Why?
Irrational Number	None	An irrational number is a number that can not be expressed as the ratio of two integers. The set of rational numbers combined with the set of irrational numbers makes up the set of real numbers.	π e √5
Integer	ℤ	An integer is a positive or negative whole number or zero. All integers are also rational numbers. This is because any integer `a` can be written `a` / 1.	4 7 √9 Why? 3.0 Why?
Natural Number	ℕ	A natural number is the set of positive integers: {1, 2, 3, …}. These are also called counting numbers. All natural numbers are also integers.	4 6/2
Table 2: Types of numbers

Properties of Numbers
Property	Description
0 - addition by	For any real or complex number `a`, `a` + 0 = 0 + `a` = `a`. See also additive identity
0 - multiplication by	For any real or complex number `a`, `a` · 0 = 0 · `a` = 0.
0 - division by	Division by zero is undefined.
1 - multiplication by	For any real or complex number `a`, 1 · `a` = `a` · 1 = `a`.
Absolute value	The absolute value of a number is the distance of a number from zero. If `a` ≥ 0, \| `a` \| = `a`. If `a` < 0, \| `a` \| = -`a`.
Addition	Addition is combining two numbers to form a sum. Addition of real and complex numbers is associative, commutative and closed.
Additive identity	The additive identity for real and complex numbers is 0 since, for any real or complex number `a`, `a` + 0 = 0 + `a` = `a`.
Additive inverse	For all real and complex numbers `a`, the additive inverse of `a` is -`a`.
Axiom of Archimedes	There is always at least one more number. For every `x` ∈ ℜ, there exists a number `n` ∈ ℜ such that `n` > `x`.
Division by 0	Division by zero is undefined.
Equality	Equality is a property that two numbers are either equal to each other or not equal to each other. Equality of numbers is symmetric, reflexive and transitive.
Multiplication	Multiplication is repeated addition. `a` · `b` = `a` + `a` + `a` + … + `a`\ `b` times. Multiplication of real and complex numbers is associative, commutative and closed.
Multiplicative identity	The multiplicative identity for real and complex numbers is 1 since, for any real or complex number `a`, `a` · 1 = 1 · `a` = `a`.
Multiplicative inverse	For all real and complex numbers `a`, the multiplicative inverse of `a` is 1 / `a`.
Ruler Postulate	The Ruler Postulate defines the association of the real numbers with a number line.

Special numbers
Name	Description
Composite number	A composite number is an integer greater than 1 that has factors other than 1 and itself.
Factorial	The factorial of n is the product of all integers from 1 to n, inclusive.
Fibonacci numbers	The Fibonacci numbers are a sequence of numbers starting with 0, 1. After the first two numbers, each number in the sequence is calculated by adding the two previous numbers.
Googol	A googol is a very large number. 1 googol = 10¹⁰⁰.
Googolplex	A googolplex is an extremely large number. 1 googolplex = 10^googol.
Prime number	A prime number is an integer greater than 1 that is divisible only by 1 and itself.

References

McAdams, David E.. All Math Words Dictionary, number. 2nd Classroom edition 20150108-4799968. pg 127. Life is a Story Problem LLC. January 8, 2015. Buy the book

More Information

McAdams, David E.. Complex Number. allmathwords.org. Life is a Story Problem LLC. 3/12/2009. https://www.allmathwords.org/en/c/complexnumber.html.

Cite this article as:

McAdams, David E. Number. 4/26/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. https://www.allmathwords.org/en/n/number.html.

Image Credits

All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Apples. Unknown.
Notched bone: Bradley J. Parker. Unknown.
Brass counters: John L. Cotter and J. Paul Hudson. Released into the public domain.

Revision History

4/26/2019: Changed equations and expressions to new format. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
9/5/2018: Removed broken links, updated license, implemented new markup. (McAdams, David E.)
8/7/2018: Changed vocabulary links to WORDLINK format. (McAdams, David E.)
8/5/2010: Added properties of numbers, special numbers. (McAdams, David E.)
12/19/2009: Added "References". (McAdams, David E.)
12/2/2008: Changed equations to images. (McAdams, David E.)
8/26/2008: In the first paragraph, organized representations of 3 into a table. (McAdams, David E.)
6/8/2008: Added types of numbers. (McAdams, David E.)
6/7/2008: Corrected spelling. (McAdams, David E.)
5/2/2008: Revised representation of irrational numbers. (McAdams, David E.)
3/22/2008: Changed Other Information to current standard. (McAdams, David E.)
11/20/2007: Initial version. (McAdams, David E.)

#	A	B	C	D
E	F	G	H	I
J	K	L	M	N
O	P	Q	R	S
T	U	V	W	X
Y	Z

All Math Words Encyclopedia is a service of Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License